题目内容
3.在△ABC中,角A,B,C的对边分别为a,b,c,asinA+bsinB-csinC=asinB.(Ⅰ)求角C的大小;
(Ⅱ)若D为AB中点,CD=1,延长CD到E,使CD=DE,设∠ACD=α,将四边形AEBC的面积S用α表示,并求S的最大值.
分析 (Ⅰ)由已知等式利用正弦定理化简可得a2+b2-c2=ab,根据余弦定理可求cosC,结合C的范围可求C的值.
(Ⅱ)依题意得四边形AEBC为平行四边形,由正弦定理得$AE=\frac{4}{{\sqrt{3}}}sinα$,$AC=\frac{4}{{\sqrt{3}}}sin(\frac{π}{3}-α)$,由三角形面积公式,三角函数恒等变换的应用化简可得S=$\frac{2\sqrt{3}}{3}$[2sin(2α+$\frac{π}{6}$)-1],由范围$0<α<\frac{π}{3}$,可求$\frac{π}{6}<2α+\frac{π}{6}<\frac{5π}{6}$,利用正弦函数的图象和性质可求四边形AEBC的面积S的最大值.
解答 解:(Ⅰ)∵asinA+bsinB-csinC=asinB.
∴得a2+b2-c2=ab,
∴$cosC=\frac{{{a^2}+{b^2}-{c^2}}}{2ab}=\frac{1}{2}$,
∴由C∈(0,π),可得:$C=\frac{π}{3}$.
(Ⅱ)依题意得△ADC≌△BDE,所以AC=BE
同理,AE=BC,所以四边形AEBC为平行四边形,
在△ACE中,由正弦定理得$\frac{AC}{{sin(\frac{π}{3}-α)}}=\frac{AE}{sina}=\frac{2}{{sin\frac{2π}{3}}}$,
所以$AE=\frac{4}{{\sqrt{3}}}sinα$,$AC=\frac{4}{{\sqrt{3}}}sin(\frac{π}{3}-α)$,
所以$S=AE•AC•sin∠EAC=\frac{16}{3}sinαsin(\frac{π}{3}-α)sin\frac{2π}{3}$=$\frac{{8\sqrt{3}}}{3}sinα(\frac{{\sqrt{3}}}{2}cosα-\frac{1}{2}sinα)$=$\frac{{8\sqrt{3}}}{3}(\frac{{\sqrt{3}}}{4}sin2α-\frac{1-cos2α}{4})$=$\frac{{2\sqrt{3}}}{3}(\sqrt{3}sin2α+cos2α-1)=\frac{{2\sqrt{3}}}{3}[{2sin(2α+\frac{π}{6})-1}]$,
因为$0<α<\frac{π}{3}$,所以$\frac{π}{6}<2α+\frac{π}{6}<\frac{5π}{6}$,
所以$2α+\frac{π}{6}=\frac{π}{2}$当,即$α=\frac{π}{6}$时,
四边形AEBC的面积S的最大值为$\frac{{2\sqrt{3}}}{3}$.
点评 本题主要考查了正弦定理,余弦定理,三角形面积公式,三角函数恒等变换的应用,正弦函数的图象和性质在解三角形中的综合应用,考查了转化思想和数形结合思想的应用,属于中档题.

| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
| A. | (0,2] | B. | (1,2] | C. | [2,4) | D. | (-4,0) |
| A. | [0,1] | B. | (-2,1] | C. | $[-\frac{7}{4},2)$ | D. | $[{-\frac{7}{4},1}]$ |
| A. | 2i | B. | -2i | C. | 2+i | D. | -2+i |
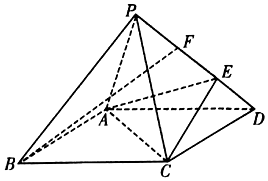 18、如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=PC=1,$PB=PD=\sqrt{2}$,E为线段PD上一点,且PE=2ED.
18、如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=PC=1,$PB=PD=\sqrt{2}$,E为线段PD上一点,且PE=2ED.