题目内容
设函数f(x)=x3+3bx2+3cx有两个极值点x1,x2,且x1∈[-1,0],x2∈[1,2],则( )
A、-10≤f(x1)≤-
| ||
B、-
| ||
C、0≤f(x1)≤
| ||
D、
|
考点:利用导数研究函数的极值
专题:综合题,导数的综合应用
分析:f(x)得f′(x)=3x2+6bx+3c由题意知方程f′(x)=0有两个根x1,x2,且x1∈[-1,0],x2∈[1,2]则由根的分布得有2b-c-1≤0,c≤0,2b+c+1≤0且4b+c+4≥0,可得-2≤c≤0,用消元法消去参数b,利用参数c表示出f(x1)的值域,再利用参数c的范围求出f(x1)的范围即可.
解答:
 解:f′(x)=3x2+6bx+3c,
解:f′(x)=3x2+6bx+3c,
由题意知方程f′(x)=0有两个根x1,x2,且x1∈[-1,0],x2∈[1,2],
则有f′(-1)≥0,f′(0)≤0,f′(1)≤0,f′(2)≥0.
即满足下列条件2b-c-1≤0,c≤0,2b+c+1≤0且4b+c+4≥0
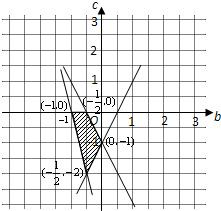
故有图中四边形ABCD即是满足这些条件的点(b,c)的区域.
所以-2≤c≤0
由题设知f'(x1)=3x12+6bx1+3c=0,
则bx1=-
x12-
c,
故f(x1)=-
x13+
x1
由于x1∈[-1,0],c≤0,
故0≤f(x1)≤
-
因为-2≤c≤0,
所以0≤f(x1)≤
.
故选:C.
 解:f′(x)=3x2+6bx+3c,
解:f′(x)=3x2+6bx+3c,由题意知方程f′(x)=0有两个根x1,x2,且x1∈[-1,0],x2∈[1,2],
则有f′(-1)≥0,f′(0)≤0,f′(1)≤0,f′(2)≥0.
即满足下列条件2b-c-1≤0,c≤0,2b+c+1≤0且4b+c+4≥0
故有图中四边形ABCD即是满足这些条件的点(b,c)的区域.
所以-2≤c≤0
由题设知f'(x1)=3x12+6bx1+3c=0,
则bx1=-
| 1 |
| 2 |
| 1 |
| 2 |
故f(x1)=-
| 1 |
| 2 |
| 3c |
| 2 |
由于x1∈[-1,0],c≤0,
故0≤f(x1)≤
| 1 |
| 2 |
| 3c |
| 2 |
因为-2≤c≤0,
所以0≤f(x1)≤
| 7 |
| 2 |
故选:C.
点评:解决此类问题的关键是熟悉导数与实根分布问题的处理方法,有难度.

练习册系列答案
相关题目
已知x、y满足约束条件
,则
的取值范围为( )
|
| y+2 |
| x+1 |
| A、[0,1] |
| B、[1,2] |
| C、[1,3] |
| D、[2,3] |
下列选项中正确的是( )
A、若
| ||||||||||||
B、若
| ||||||||||||
C、若
| ||||||||||||
D、
|
已知f(x)=log3x,则f(
),f(
),f(2)的大小是( )
| 1 |
| 4 |
| 1 |
| 2 |
A、f(
| ||||
B、f(
| ||||
C、f(
| ||||
D、f(2)>f(
|
已知f(x)是定义在实数集R上的函数,f(1)=-
且f(x+1)[1-f(x)]=1+f(x),则f(2010)=( )
| 3 |
A、2+
| ||
B、
| ||
C、
| ||
D、-
|
在矩形ABCD中,|
|=4
,设
=
,
=
,
=
,则|
+
+
|=( )
| AD |
| 3 |
| AB |
| a |
| BC |
| b |
| BD |
| c |
| a |
| b |
| c |
A、4
| ||
B、
| ||
C、8
| ||
D、2
|
{a,b}的真子集个数为( )
| A、4 | B、3 | C、2 | D、1 |