题目内容
已知变量x、y满足
,则z=
的取值范围是 .
|
| x2+y2 |
考点:简单线性规划
专题:不等式的解法及应用
分析:画出可行域再根据可行域的位置看可行域当中的点什么时候与原点的距离最远什么时候与原点的距离最近,最后注意此题求解的是距离的范围,进而得到最终答案.
解答:
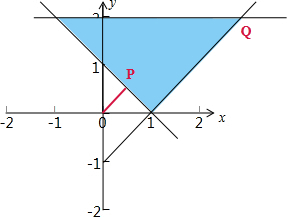 解:由题意可知,线性约束条件
解:由题意可知,线性约束条件
对应的可行域如下,
由图可知原点到Q(3,2)的距离最远为:
=
,
原点到P的距离最近,即原点到直线x+y=1的距离为
=
,
故z=
的范围是[
,
].
故答案为:[
,
].
 解:由题意可知,线性约束条件
解:由题意可知,线性约束条件
|
由图可知原点到Q(3,2)的距离最远为:
| 32+22 |
| 13 |
原点到P的距离最近,即原点到直线x+y=1的距离为
| 1 | ||
|
| ||
| 2 |
故z=
| x2+y2 |
| ||
| 2 |
| 13 |
故答案为:[
| ||
| 2 |
| 13 |
点评:本题考查的是线性规划问题.在解答此类问题时,首先根据线性约束条件画出可行域,再根据可行域分析问题.同时在本题中的目标函数充分与几何意义联合考查,规律强易出错值得同学们反思总结.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
设函数f(x)=x3+3bx2+3cx有两个极值点x1,x2,且x1∈[-1,0],x2∈[1,2],则( )
A、-10≤f(x1)≤-
| ||
B、-
| ||
C、0≤f(x1)≤
| ||
D、
|