题目内容
10.已知数列{an}的前n项和Sn和通项an满足Sn=$\frac{1}{2}$(1-an).(1)求数列{an}的通项公式;
(2)设函数f(x)=log${\;}_{\frac{1}{3}}$x,bn=f(a1)+f(a2)+…+f(an),Tn=$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+$\frac{1}{{b}_{3}}$+…+$\frac{1}{{b}_{n}}$,求Tn的取值范围.
分析 由Sn=$\frac{1}{2}$(1-an)知,当n≥2时,an=Sn-Sn-1=-$\frac{1}{2}$an+$\frac{1}{2}$an-1,整理可得$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{1}{3}$,由S1=a1=$\frac{1}{2}$(1-a1)⇒a1=$\frac{1}{3}$,从而可知数列{an}是首项为$\frac{1}{3}$,公比为$\frac{1}{3}$的等比数列,于是可求得数列{an}的通项
解答 解:(1)因为Sn=$\frac{1}{2}$(1-an),
所以,当n≥2时,an=Sn-Sn-1=$\frac{1}{2}$(1-an)-$\frac{1}{2}$(1-an-1)=-$\frac{1}{2}$an+$\frac{1}{2}$an-1,
化简得2an=-an+an-1,整理可得$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{1}{3}$,由S1=a1=$\frac{1}{2}$(1-a1)⇒a1=$\frac{1}{3}$,从而可知数列{an}是首项为$\frac{1}{3}$,公比为$\frac{1}{3}$的等比数列.
所以an=$\frac{1}{3}$×($\frac{1}{3}$)n-1=($\frac{1}{3}$)n.
(2)函数f(x)=log${\;}_{\frac{1}{3}}$x,bn=f(a1)+f(a2)+…+f(an)=1+2+3+4…+n=$\frac{n(n+1)}{2}$,Tn=$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+$\frac{1}{{b}_{3}}$+…+$\frac{1}{{b}_{n}}$=2(1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$+…$\frac{1}{n}-\frac{1}{n+1}$)=2(1-$\frac{1}{n+1}$)=$\frac{2n}{n+1}$,所以Tn的取值范围为[1,2).
点评 本题考查数列递推式的应用,得到数列为等比数列,进一步通过对数运算得到得到f(an),Tn是关键,考查等比关系的确定及其通项公式的应用,属于中档题

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案| A. | {-2,-1,0} | B. | (-1,0) | C. | {-1,0} | D. | (-3,-2) |
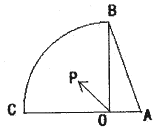 已知在Rt△AOB中,AO=1,BO=2,如图,动点P是在以O点为圆心,OB为半径的扇形内运动(含边界)且∠BOC=90°;设$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,则x+y的取值范围[-2,1].
已知在Rt△AOB中,AO=1,BO=2,如图,动点P是在以O点为圆心,OB为半径的扇形内运动(含边界)且∠BOC=90°;设$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,则x+y的取值范围[-2,1].