题目内容
20.设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点(0,$\sqrt{3}$),离心率为$\frac{1}{2}$.(1)求椭圆C的方程;
(2)求过点(1,0)且斜率为1的直线被椭圆C所截线段的长度.
分析 (1)求出b,根据e2=1-$\frac{{b}^{2}}{{a}^{2}}$=$\frac{1}{4}$,求出a的值,所以即可得到椭圆方程.
(2)求出直线l的方程,联立直线与椭圆方程,根据弦长公式求出线段的长度即可.
解答 解:(1)依题意有b=$\sqrt{3}$,e2=1-$\frac{{b}^{2}}{{a}^{2}}$=$\frac{1}{4}$,所以a=2,
所求方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)由题意直线l:y=x-1,设l交椭圆于A(x1,y1),B(x2,y2)两点,
由$\left\{\begin{array}{l}{y=x-1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$消去y得7x2-8x-8=0,
∴x1+x2=$\frac{8}{7}$,x1x2=-$\frac{8}{7}$,
所以根据弦长公式得到AB=$\sqrt{1{+k}^{2}}$|x1-x2|=$\frac{24}{7}$.
点评 本题考查椭圆方程的求法,直线与椭圆的位置关系的综合应用,考查转化思想以及计算能力.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
11.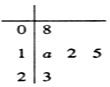 如图是一名篮球运动员在最近5场比赛中所得分数的茎叶图,若该运动员在这5场比赛中的得分的中位数为12,则该运动员这5场比赛得分的平均数不可能为( )
如图是一名篮球运动员在最近5场比赛中所得分数的茎叶图,若该运动员在这5场比赛中的得分的中位数为12,则该运动员这5场比赛得分的平均数不可能为( )
 如图是一名篮球运动员在最近5场比赛中所得分数的茎叶图,若该运动员在这5场比赛中的得分的中位数为12,则该运动员这5场比赛得分的平均数不可能为( )
如图是一名篮球运动员在最近5场比赛中所得分数的茎叶图,若该运动员在这5场比赛中的得分的中位数为12,则该运动员这5场比赛得分的平均数不可能为( )| A. | $\frac{68}{5}$ | B. | $\frac{69}{5}$ | C. | 14 | D. | $\frac{71}{5}$ |
8.在某项体育比赛中,五位裁判为一选手打出的分数如下:
92 89 95 91 93
去掉一个最高分和一个最低分后,所剩数的平均值和方差分别为( )
92 89 95 91 93
去掉一个最高分和一个最低分后,所剩数的平均值和方差分别为( )
| A. | 92,4 | B. | 93,5 | C. | 93,4 | D. | 92,$\frac{2}{3}$ |
9.若命题p:?x0>0,|x0|≤1,则命题p的否定是( )
| A. | ?x>0,|x|>1 | B. | ?x>0,|x|≥1 | C. | ?x≤0,|x|<1 | D. | ?x≤0,|x|≤1 |
10.若存在实数α∈R,$β∈[\frac{π}{2},π]$,使得实数t同时满足$t={cos^2}β+\frac{α}{2}cosβ$,α≤t≤α-2cosβ,则t的取值范围是( )
| A. | $[-\frac{2}{3},0]$ | B. | $[0,\frac{4}{3}]$ | C. | $[\frac{4}{3},2]$ | D. | [2,4] |