题目内容
2.设函数fn(x)=-xn+3ax+b(n∈N*,a,b∈R),若|f4(x)|在[-1,1]上的最大值为$\frac{1}{2}$,则a+b=$\frac{1}{2}$.分析 由题意知|f4(0)|=|b|≤$\frac{1}{2}$,|f4(-1)|=|-1-3a+b|≤$\frac{1}{2}$,|f4(1)|=|-1+3a+b|≤$\frac{1}{2}$,从而解得.
解答 解:由题意知,f4(x)=-x4+3ax+b,
∵|f4(x)|在[-1,1]上的最大值为$\frac{1}{2}$,
∴|f4(0)|=|b|≤$\frac{1}{2}$,
|f4(-1)|=|-1-3a+b|≤$\frac{1}{2}$,
|f4(1)|=|-1+3a+b|≤$\frac{1}{2}$,
讨论可知|-1-3a+b|与|-1+3a+b|中至少有一个为|3a|+|b-1|,
故|3a|+|b-1|≤$\frac{1}{2}$,
故a=0,b=$\frac{1}{2}$;
故a+b=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查了转化思想的应用及绝对值不等式的解法,属于中档题.

练习册系列答案
相关题目
13.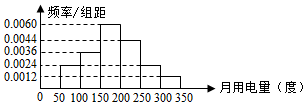 为了了解长沙市居民月用电情况,抽查了该市100户居民用电量(单位:度),得到频率分布直方图如下:根据如图可得到这100户居民月用电量在[150,300]的用户数是( )
为了了解长沙市居民月用电情况,抽查了该市100户居民用电量(单位:度),得到频率分布直方图如下:根据如图可得到这100户居民月用电量在[150,300]的用户数是( )
 为了了解长沙市居民月用电情况,抽查了该市100户居民用电量(单位:度),得到频率分布直方图如下:根据如图可得到这100户居民月用电量在[150,300]的用户数是( )
为了了解长沙市居民月用电情况,抽查了该市100户居民用电量(单位:度),得到频率分布直方图如下:根据如图可得到这100户居民月用电量在[150,300]的用户数是( )| A. | 70 | B. | 64 | C. | 48 | D. | 30 |
4.已知i为虚数单位,若复数i•z=$\sqrt{2}$-i,则|z|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
1.已知集合P={x|x2-2x-3≥0},Q={x|1<x<4},则P∩Q=( )
| A. | {x|-1<x<3} | B. | {x|3≤x<4} | C. | {x|x≥4或x<-3} | D. | {x|x<-1或x>3} |
2.已知随机变量X~N(1,σ2),若P(0<X<2)=0.4,则P(X≤0)=( )
| A. | 0.6 | B. | 0.4 | C. | 0.3 | D. | 0.2 |
 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(0)=$\frac{{\sqrt{6}}}{2}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(0)=$\frac{{\sqrt{6}}}{2}$.