题目内容
已知椭圆C:
+
=1(a>b>0)的离心率e=
,点F是椭圆的左焦点,A为椭圆的右顶点,B为椭圆的上顶点,且
•
=
+1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P(x0,y0)关于直线2x-y=0的对称点P′在椭圆C上,求z=4x0+3y0的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| FB |
| FA |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P(x0,y0)关于直线2x-y=0的对称点P′在椭圆C上,求z=4x0+3y0的取值范围.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:(1)根据F(-c,0),A(A,0),B(0,b).由
•
=
+1得,ac+c2=
+1.e=
,解方程求解.
(2)设点P(x′,y′),则
,解得
,代入椭圆的方程,根据自变量的范围求解.
| FB |
| FA |
| 2 |
| 2 |
| ||
| 2 |
(2)设点P(x′,y′),则
|
|
解答:
解:(Ⅰ)设焦距为2c(c>0),则F(-c,0),A(A,0),B(0,b).
由
•
=
+1得,ac+c2=
+1.
又∵e=
=
,解得a=
,c=1,∴b=1.
∴椭圆C的方程为
+y2=1.
(Ⅱ)设点P(x′,y′),则
,解得
∴z=4x0+3y0=5y′.
∵P(x′,y′)在椭圆C上,∴-1≤y′≤1,
∴-5≤z≤5,即z=4x0+3y0的取值范围为[-5,5].
由
| FB |
| FA |
| 2 |
| 2 |
又∵e=
| c |
| a |
| ||
| 2 |
| 2 |
∴椭圆C的方程为
| x2 |
| 2 |
(Ⅱ)设点P(x′,y′),则
|
|
∴z=4x0+3y0=5y′.
∵P(x′,y′)在椭圆C上,∴-1≤y′≤1,
∴-5≤z≤5,即z=4x0+3y0的取值范围为[-5,5].
点评:本题考查了椭圆的方程,定义,直线与椭圆的位置关系,运算仔细认真.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
下面不等式不成立的是( )
| A、90.7<90.8 | ||||
B、(
| ||||
| C、53.1<33.1 | ||||
| D、1.80.6>0.81.6 |
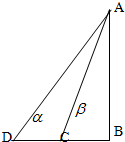 如图:D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点仰角分别是β,α(α<β),则A点离地面的高度AB等于
如图:D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点仰角分别是β,α(α<β),则A点离地面的高度AB等于