题目内容
为选拔选手参加“中国汉字听写大会”,某中学举行了一次“汉字听写大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).
(1)求样本容量n和频率分布直方图中的x、y的值;
(理科)(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取3名学生参加“中国汉字听写大会”,设随机变量X表示所抽取的3名学生中得分在[80,90,)内的学生人数,求随机变量X的分布列及数学期望.
(文科)(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“中国汉字听写大会”,求所抽取的2名学生中至少有一人得分在[90,100]内的概率.

(1)求样本容量n和频率分布直方图中的x、y的值;
(理科)(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取3名学生参加“中国汉字听写大会”,设随机变量X表示所抽取的3名学生中得分在[80,90,)内的学生人数,求随机变量X的分布列及数学期望.
(文科)(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“中国汉字听写大会”,求所抽取的2名学生中至少有一人得分在[90,100]内的概率.
考点:频率分布直方图,列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)由频率公式和图求出样本容量n,由频率分布直方图中的数据求出x、y的值;
(2)理科:先求出分数在[80,90)、[90,100]内的学生人数,求出抽取的3名学生中得分在[80,90)的人数X的可能取值,由概率公式分别求出它们的概率并列出X的分布列,代入公式求出EX;
文科:先对7名学生分类进行编号,列出所有的基本事件,再列出2名同学的分数都不在[90,100]内的情况,
利用概率公式和对立事件的概率公式求出即可.
(2)理科:先求出分数在[80,90)、[90,100]内的学生人数,求出抽取的3名学生中得分在[80,90)的人数X的可能取值,由概率公式分别求出它们的概率并列出X的分布列,代入公式求出EX;
文科:先对7名学生分类进行编号,列出所有的基本事件,再列出2名同学的分数都不在[90,100]内的情况,
利用概率公式和对立事件的概率公式求出即可.
解答:
解:(1)由题意可知,样本容量n=
=50,y=
=0.004,
x=0.100-0.004-0.010-0.016-0.040=0.030.…(4分)
(理科)(2)由题意可知,分数在[80,90)内的学生有5人,分数在[90,100]内的学生有2人,共7人.
抽取的3名学生中得分在[80,90)的人数X的可能取值为1,2,3,则
P(X=1)=
=
=
,P(X=2)=
=
=
,P(X=3)=
=
=
.
所以X的分布列为
所以EX=1×
+2×
+3×
=
.…(12分)
(文科)(2)由题意可知,分数在[80,90)内的学生有5人,记这5人分别为1、2、3、4、5,
分数在[90,100]内的学生有2人,记这2人分别为a、b.
抽取的2名学生的所有情况有21种,分别为:
(1,2),(1,3),(1,4),(1,5),(1,a),(1,b),(2,3),
(2,4),(2,5),(2,a),(2,b),(3,4),(3,5),(3,a),
(3,b),(4,5),(4,a),(4,b),(5,a),(5,b),(a,b).(8分)
其中2名同学的分数都不在[90,100]内的情况有10种,分别为:
(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),
(3,4),(3,5),(4,5).
∴所抽取的2名学生中至少有一人得分在[90,100]内的概率P=1-
=
.…(12分)
| 8 |
| 0.016×10 |
| 2 |
| 50×10 |
x=0.100-0.004-0.010-0.016-0.040=0.030.…(4分)
(理科)(2)由题意可知,分数在[80,90)内的学生有5人,分数在[90,100]内的学生有2人,共7人.
抽取的3名学生中得分在[80,90)的人数X的可能取值为1,2,3,则
P(X=1)=
| ||||
|
| 5 |
| 35 |
| 1 |
| 7 |
| ||||
|
| 20 |
| 35 |
| 4 |
| 7 |
| ||||
|
| 10 |
| 35 |
| 2 |
| 7 |
所以X的分布列为
| X | 1 | 2 | 3 | ||||||
| P |
|
|
|
| 1 |
| 7 |
| 4 |
| 7 |
| 2 |
| 7 |
| 15 |
| 7 |
(文科)(2)由题意可知,分数在[80,90)内的学生有5人,记这5人分别为1、2、3、4、5,
分数在[90,100]内的学生有2人,记这2人分别为a、b.
抽取的2名学生的所有情况有21种,分别为:
(1,2),(1,3),(1,4),(1,5),(1,a),(1,b),(2,3),
(2,4),(2,5),(2,a),(2,b),(3,4),(3,5),(3,a),
(3,b),(4,5),(4,a),(4,b),(5,a),(5,b),(a,b).(8分)
其中2名同学的分数都不在[90,100]内的情况有10种,分别为:
(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),
(3,4),(3,5),(4,5).
∴所抽取的2名学生中至少有一人得分在[90,100]内的概率P=1-
| 10 |
| 21 |
| 11 |
| 21 |
点评:本题考查茎叶图、频率分布直方图,随机变量X的分布列及数学期望,以及古典概型,比较综合.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
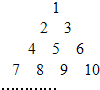 如图,自然数列按正三角形图顺序排列,如数9排在第4行第3个位置;设数2015排在第m行第n个位置,则m+n=
如图,自然数列按正三角形图顺序排列,如数9排在第4行第3个位置;设数2015排在第m行第n个位置,则m+n=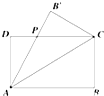 某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用,如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB′交DC于点P,经试验当△ADP的面积最大时最节能.
某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用,如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB′交DC于点P,经试验当△ADP的面积最大时最节能. 如图,在正方体ABCD-A′B′C′D′中,E是棱BC的中点,F是对角线A′C的中点,设
如图,在正方体ABCD-A′B′C′D′中,E是棱BC的中点,F是对角线A′C的中点,设