题目内容
13.在△ABC中,若a=$3\sqrt{2}$,cosC=$\frac{1}{3}$,S△ABC-=4$\sqrt{2}$,则b等于( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 4$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 利用同角三角函数的关系计算sinC,根据面积公式S=$\frac{1}{2}absinC$列方程解出b.
解答 解:sinC=$\sqrt{1-co{s}^{2}C}=\frac{2\sqrt{2}}{3}$,
∵S△ABC=$\frac{1}{2}absinC$=$\frac{1}{2}×3\sqrt{2}b×\frac{2\sqrt{2}}{3}$=4$\sqrt{2}$.
∴b=2$\sqrt{2}$.
故选:D.
点评 本题考查了同角三角函数的关系,三角形的面积公式,属于基础题.

练习册系列答案
相关题目
3.已知i为虚数单位,若复数z满足|z-3-4i|=1,则|z|的最大值为( )
| A. | 4 | B. | 5 | C. | 4$\sqrt{2}$ | D. | 6 |
18.圆x2+y2-2x+4y-11=0的半径为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
2.如图在平行四边形ABCD中,E、F分别是AB、BC边中点,线段CE、DF相交于点G,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{AG}$=( )
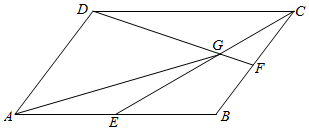

| A. | $\frac{4}{5}$$\overrightarrow{a}$+$\frac{3}{5}$$\overrightarrow{b}$ | B. | $\frac{3}{5}$$\overrightarrow{a}$+$\frac{4}{5}$$\overrightarrow{b}$ | C. | $\frac{5}{6}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{5}{6}$$\overrightarrow{b}$ |