题目内容
14.已知命题p:直线l1:x-2y+3=0与l2:2x+y+3=0相交但不垂直;命题q:?x0∈(0,+∞),x0+2>ex0,则下列命题中是真命题的是( )| A. | (?p)∧q | B. | p∧q | C. | p∨(?q) | D. | (?p)∧(?q) |
分析 判断两个命题的真假,然后判断命题的否定命题的真假,利用复合命题判断即可.
解答 解:命题p:直线l1:x-2y+3=0与l2:2x+y+3=0相交并且垂直;所以命题p是假命题;则¬p是真命题;
命题q:?x0∈(0,+∞),x0+2>ex0,因为x0=1时,命题是真命题,所以q是真命题,¬p是假命题;
则:(?p)∧q是真命题;p∧q、p∨(?q)、(?p)∧(?q)都是假命题;
故选:A.
点评 本题考查命题的真假的判断与应用,是基本知识的考查.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
2.在△ABC中,内角A,B,C的对边分别是a,b,c,向量$\overrightarrow m=({\frac{a}{2},\frac{c}{2}}),\overrightarrow n=({cosC,cosA})$,且$\overrightarrow n•\overrightarrow m=bcosB$则B的值是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
6.设z=x+y,其中x,y满足$\left\{\begin{array}{l}x+2y≥0\\ 2x-y≤0\\ 0≤y≤m\end{array}\right.$,若z的最大值为12,则z的最小值为( )
| A. | -8 | B. | -6 | C. | 6 | D. | 8 |
3.若sinθ,cosθ是方程4x2+2mx+m=0的两根,则m的值为( )
| A. | .$1+\sqrt{5}$ | B. | .$1-\sqrt{5}$ | C. | $.1±\sqrt{5}$ | D. | .$-1-\sqrt{5}$ |
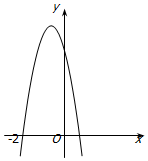 已知函数f(x)=ax3+bx2+4x的极小值为-8,其导函数y=f'(x)的图象经过点(-2,0),如图所示.
已知函数f(x)=ax3+bx2+4x的极小值为-8,其导函数y=f'(x)的图象经过点(-2,0),如图所示.