题目内容
20.设x,y满足约束条件$\left\{\begin{array}{l}{x-1≥0}\\{x-y≤0}\\{x+y-4≤0}\end{array}\right.$,则目标函数z=$\frac{x+2y-1}{x+1}$的最大值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | 3 | D. | 4 |
分析 作出不等式组对应的平面区域,化简目标函数,利用线性规划的知识即可得到结论.
解答 解:x,y满足约束条件$\left\{\begin{array}{l}{x-1≥0}\\{x-y≤0}\\{x+y-4≤0}\end{array}\right.$的可行域如图:
则目标函数z=$\frac{x+2y-1}{x+1}$=1+2$•\frac{y-1}{x+1}$,几何意义是可行域内的点与(-1,1)类型的斜率的2倍加1,
由可行域可知AD类型的斜率最大,由$\left\{\begin{array}{l}{x=1}\\{x+y=4}\end{array}\right.$可得A(1,3),
则目标函数z=$\frac{x+2y-1}{x+1}$的最大值为:$\frac{1+2×3-1}{1+1}$=3.
故选:C.
点评 本题主要考查线性规划的应用,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
10.已知x为实数,则“$\frac{1}{x}<1$”是“x>1”的( )
| A. | 充分非必要条件 | B. | 充要条件 | ||
| C. | 必要非充分条件 | D. | 既不充分也不必要条件 |
8.已知f(x)=$\left\{\begin{array}{l}{x^2}-131,x>10\\ f(f(x+2)),x≤10\end{array}\right.$,则f(8)的值为( )
| A. | 13 | B. | -67 | C. | 1313 | D. | -6767 |
15.已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF,若|AB|=10,|AF|=6,cos∠FAB=$\frac{3}{5}$,则C的离心率为( )
| A. | $\frac{7}{5}$ | B. | $\frac{5}{7}$ | C. | $\frac{4}{5}$ | D. | $\frac{6}{7}$ |
10.为了判断高中生的文理科选修是否与性别有关,随机调查了50名学生,得到如下2×2列联表:
(1)画出列联表的等高条形图,并通过图形判断文理科选修与性别是否有关?
(2)利用列联表的独立性检验,能否在犯错误的概率不超过0.05的前提下认为选修文理科与性别有关?
| 理科 | 文科 | |
| 男 | 14 | 10 |
| 女 | 6 | 20 |
(2)利用列联表的独立性检验,能否在犯错误的概率不超过0.05的前提下认为选修文理科与性别有关?
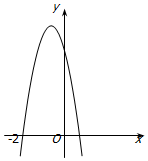 已知函数f(x)=ax3+bx2+4x的极小值为-8,其导函数y=f'(x)的图象经过点(-2,0),如图所示.
已知函数f(x)=ax3+bx2+4x的极小值为-8,其导函数y=f'(x)的图象经过点(-2,0),如图所示.