题目内容

∫
 
2
0
（cos
π
2
x+
4-x2
）dx的值为（　　）
A、2π
B、π
C、π+1
D、π+
2
π
考点：定积分
专题：导数的概念及应用
分析：根据定积分的计算和定积分的几何意义，计算可得．
解答： 解：∫
 
2
0
4-x2
）dx的几何意义是以原点为圆心，以2为半径的圆的面积的四分之一，
故∫
 
2
0
4-x2
=
1
4
×4π=π，
所以∫
 
2
0
（cos
π
2
x+
4-x2
）dx=∫
 
2
0
cos
π
2
xdx+∫
 
2
0
4-x2
dx=
2
π
sin
πx
2
|
2
0
+π=π．
故选：B
点评：本题主要考查了微积分基本定理和定积分的几何意义，属于基础题．
练习册系列答案
相关题目
函数y=lg（sinx+cosx）的单调递增区间是（　　）
A、[2kπ-
3π
4
，2kπ+
3π
4
]，k∈Z
B、（2kπ-
π
4
，2kπ+
π
4
]，k∈Z
C、[2kπ+
π
4
，2kπ+
5π
4
]，k∈Z
D、[2kπ+
π
4
，2kπ+
3π
4
]，k∈Z
已知（x，y）满足
x-y+1≥0
x+y-2≥0
x≤m
，且x-3y的最大值不小于6，则实数m的取值范围是（　　）
A、（-∞，3]
B、[3，+∞）
C、（-∞，
9
2
]
D、[
9
2
，+∞）
若α是第二象限角，且tan（π-α）=
1
2
，则cos（
3π
2
-α）=（　　）
A、
3
2
B、-
3
2
C、
5
5
D、-
5
5
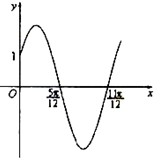已知函数f（x）=Asin（ωx+φ）（x∈R，ω＞0，0＜ω＜
π
2
）的部分图象如图所示．则函数f（x）的解析式为（　　）
A、f（x）=2sin（2x+
π
6
）
B、f（x）=2sin（2x+
π
3
）
C、f（x）=2sin（2x-
π
6
）
D、f（x）=2sin（2x-
π
3
）
已知正四棱锥P-ABCD的侧棱与底面所成角为60°，M为PA中点，连结DM，则DM与平面PAC所成角的大小是（　　）
A、30°B、45°
C、60°D、90°
顶点在原点，坐标轴为对称轴的抛物线过点（-2，3），则它的方程是（　　）
A、x2=
4
3
y或y2=-
9
2
x
B、x2=±8y或x2=
4
3
y
C、x2=
4
3
y
D、y2=-
9
2
x
已知直线l1：2x-3y+1=0，l2：x+y-2=0的交点为P．
（1）求点P的坐标；
（2）求过点P且与直线l2垂直的直线l的方程．
已知i是虚数单位，m∈R，z=m（m-1）+（m2+2m-3）i．
（Ⅰ）若z是纯虚数，求m的值；
（Ⅱ）若在复平面C内，z所对应的点在第四象限，求m的取值范围；
（Ⅲ）当m=2时，z是关于x的方程x2+px+q=0的一个根，求实数p，q的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网