题目内容
已知正四棱锥P-ABCD的侧棱与底面所成角为60°,M为PA中点,连结DM,则DM与平面PAC所成角的大小是( )
| A、30° | B、45° |
| C、60° | D、90° |
考点:直线与平面所成的角
专题:空间角
分析:要求线面角,关键找到面PAC的垂线,即BD,从而∠DMO即是,然后在三角形中计算角的大小.
解答:
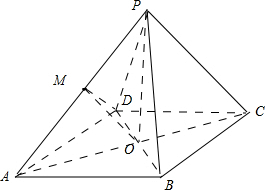 解:连接AC、BD,AC∩BD=O,连接MO,设AB=a,∵正四棱锥P-ABCD,∴,PO⊥面ABCD,BD?面ABCD,PO⊥BD,BD⊥AC,又∵PO∩AC=O,∴BD⊥面PAC,∴∠DMO即DM与平面PAC所成角.
解:连接AC、BD,AC∩BD=O,连接MO,设AB=a,∵正四棱锥P-ABCD,∴,PO⊥面ABCD,BD?面ABCD,PO⊥BD,BD⊥AC,又∵PO∩AC=O,∴BD⊥面PAC,∴∠DMO即DM与平面PAC所成角.
AB=a,AO=
a,又侧棱与底面所成角为60°,即∠PAO=60°,在Rt△PAO中,PA=
a,M为PA中点,∴OM=
PA=
a,在Rt△DMO中,DO=
a,OM=
a,∴∠DMO=45°
故选:B.
 解:连接AC、BD,AC∩BD=O,连接MO,设AB=a,∵正四棱锥P-ABCD,∴,PO⊥面ABCD,BD?面ABCD,PO⊥BD,BD⊥AC,又∵PO∩AC=O,∴BD⊥面PAC,∴∠DMO即DM与平面PAC所成角.
解:连接AC、BD,AC∩BD=O,连接MO,设AB=a,∵正四棱锥P-ABCD,∴,PO⊥面ABCD,BD?面ABCD,PO⊥BD,BD⊥AC,又∵PO∩AC=O,∴BD⊥面PAC,∴∠DMO即DM与平面PAC所成角.AB=a,AO=
| ||
| 2 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
故选:B.
点评:本题考查线面角的计算,遵循先作后算的原则.

练习册系列答案
相关题目
若集合A={-1,0,1,2,3},集合B={x|x∈A,1-x∉A},则集合B的元素的个数为( )
| A、0 | B、1 | C、2 | D、3 |
如图所示的程序输出的结果为( )


| A、17 | B、19 | C、21 | D、23 |
阅读程序(如图),若a=45,b=20,c=10,则输出的结果为( )


| A、10 | B、20 | C、25 | D、45 |
∫
(cos
x+
)dx的值为( )
2 0 |
| π |
| 2 |
| 4-x2 |
| A、2π | ||
| B、π | ||
| C、π+1 | ||
D、π+
|
已知△ABC中,|
|=10,
•
=-16,D为边BC的中点,则|
|等于( )
| BC |
| AB |
| AC |
| AD |
| A、6 | B、5 | C、4 | D、3 |
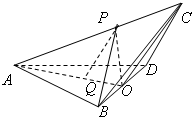 如图,三棱锥C-ABD中,AB=AD=BD=BC=CD=2,O为BD的中点,∠AOC=120°,P为AC上一点,Q为AO上一点,且
如图,三棱锥C-ABD中,AB=AD=BD=BC=CD=2,O为BD的中点,∠AOC=120°,P为AC上一点,Q为AO上一点,且