题目内容
1．已知角A是△ABC的一个内角，若sin A+cos A=$\frac{3}{5}$，则sinA-cosA等于$\frac{{\sqrt{41}}}{5}$．分析 利用同角三角函数的基本关系，以及三角函数在各个象限中的符号，求得sinA-cosA的值．
解答 解：∵角A是△ABC的一个内角，若sin A+cos A=$\frac{3}{5}$，
∴1+2sinAcosA=$\frac{9}{25}$，∴sinAcosA=-$\frac{8}{25}$，∴A为钝角，
则sinA-cosA=$\sqrt{{（sinA-cosA）}^{2}}$=$\sqrt{1-2sinAcosA}$=$\sqrt{1-2•（-\frac{8}{25}）}$=$\frac{\sqrt{41}}{5}$，
故答案为：$\frac{\sqrt{41}}{5}$．
点评 本题主要考查同角三角函数的基本关系，以及三角函数在各个象限中的符号，属于基础题．
练习册系列答案
相关题目
16．某企业共有职工150人，其中高级职称15人，中级职称45人，初级职称90人，现用分层抽样方法抽取一个容量为30的样本，则各职称中抽取的人数分别为（ ）
| A． | 5，10，15 | B． | 3，9，18 | C． | 5，9，16 | D． | 3，10，17 |
13．$\overrightarrow{a}$，$\overrightarrow{b}$都为向量，则下列式子正确的是（ ）
| A． | $\overrightarrow{a}$•|$\overrightarrow{a}$|=$\overrightarrow{a}$2 | B． | （$\overrightarrow{a}$•$\overrightarrow{b}$）2=$\overrightarrow{a}$2•$\overrightarrow{b}$2 | C． | （$\overrightarrow{a}$•$\overrightarrow{b}$）$\overrightarrow{c}$=$\overrightarrow{a}$（$\overrightarrow{b}$•$\overrightarrow{c}$） | D． | |$\overrightarrow{a}$•$\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$| |
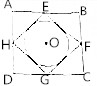已知四边形ABCD中，E，F，G，H分别是线段AB，BC，CD，DA的中点，圆O为四边形EFGH的内切圆，则在正方形ABCD内投一点，该点落在圆O内的概率为$\frac{π}{8}$．