题目内容
在△ABC中,角A、B、C的对边分别为a、b、c,且A、B、C成等差数列.
(Ⅰ)角B的大小;
(Ⅱ)若a=2,△ABC的面积SV=2
,求b、c的长及△ABC外接圆半径.
(Ⅰ)角B的大小;
(Ⅱ)若a=2,△ABC的面积SV=2
| 3 |
考点:正弦定理,余弦定理
专题:解三角形
分析:(Ⅰ)由A、B、C成等差数列以及A+B+C=π,求得B的值.
(Ⅱ)由△ABC的面积S=
ac•sinB=2
,求得c的值.再由余弦定理求得b的值,再由正弦定理可得三角形外接圆的半径R的值.
(Ⅱ)由△ABC的面积S=
| 1 |
| 2 |
| 3 |
解答:
解:(Ⅰ)△ABC中,由A、B、C成等差数列,可得2B=A+C,
再根据A+B+C=π,求得 B=
,A+C=
.
(Ⅱ)若a=2,则由△ABC的面积SV=
ac•sinB=
•2•c•
=2
,求得c=4.
再由余弦定理可得b2=a2+c2-2ac•cosB=4+16-16•
=12 b=2
.
设△ABC外接圆半径为R,则由正弦定理可得2R=
=
=4,
解得R=2.
再根据A+B+C=π,求得 B=
| π |
| 3 |
| 2π |
| 3 |
(Ⅱ)若a=2,则由△ABC的面积SV=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
再由余弦定理可得b2=a2+c2-2ac•cosB=4+16-16•
| 1 |
| 2 |
| 3 |
设△ABC外接圆半径为R,则由正弦定理可得2R=
| b |
| sinB |
2
| ||||
|
解得R=2.
点评:本题主要考查正弦定理和余弦定理的应用,等差数列的定义和性质,属于基础题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
已知单位向量
、
的夹角为60°,则|
+
|的值为( )
| a |
| b |
| a |
| b |
| A、3 | ||
| B、2 | ||
C、
| ||
D、
|
已知x>1,则函数f(x)=4x+
+1的最小值是( )
| 1 |
| x-1 |
| A、7 | B、9 | C、11 | D、13 |
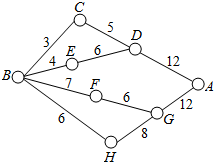 如图,小圆圈表示网络的结点,结点之间的连线表示它们有网相联.连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点B向结点A传递信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )
如图,小圆圈表示网络的结点,结点之间的连线表示它们有网相联.连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点B向结点A传递信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )