题目内容
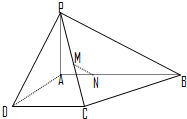 如图所示,在四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=DC=
如图所示,在四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=DC=| 1 |
| 2 |
| 1 |
| 3 |
(Ⅰ)证明:MN∥平面PAD;
(Ⅱ)求三棱锥B-PNC的体积.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(Ⅰ)过M在平面PCD内作ME∥DC交PD于E,连接AE,证明EMAN为平行四边形,可得MN∥AE,即可证明MN∥平面PAD;
(Ⅱ)利用VB-PNC=VP-BNC=
S△BNC•PA,即可求三棱锥B-PNC的体积.
(Ⅱ)利用VB-PNC=VP-BNC=
| 1 |
| 3 |
解答:
(Ⅰ)证明:过M在平面PCD内作ME∥DC交PD于E,连接AE,
则ME平行且等于
DC,…(2分)
又DC=1,∴ME=
又AB⊥AD,AD⊥DC,∴DC∥AB
又AN=
NB=
AB=
,∴ME平行且等于AN,
∴EMAN为平行四边形 …(4分)
∴MN∥AE,∴MN∥平面PAD,…(6分)
(Ⅱ)解:∵PA⊥底面ABCD,
∴VB-PNC=VP-BNC=
S△BNC•PA=
.…(12分)
则ME平行且等于
| 1 |
| 2 |
又DC=1,∴ME=
| 1 |
| 2 |
又AB⊥AD,AD⊥DC,∴DC∥AB
又AN=
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
∴EMAN为平行四边形 …(4分)
∴MN∥AE,∴MN∥平面PAD,…(6分)
(Ⅱ)解:∵PA⊥底面ABCD,
∴VB-PNC=VP-BNC=
| 1 |
| 3 |
| 1 |
| 4 |
点评:本题考查直线与平面平行的判定,考查三棱锥B-PNC的体积,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知直线m,n和平面α,满足m?α,n∥α,则直线m,n的关系是( )
| A、平行 | B、相交 |
| C、异面 | D、平行或异面 |
若向量
、
的坐标满
+
=(-2,-1,2),
-
=(4,-3,-2),则
•
的等于( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、5 | B、-5 | C、7 | D、-1 |
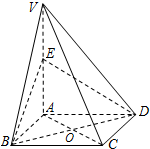 如图,在四棱锥V-ABCD中,底面ABCD是正方形,侧棱VA⊥底面ABCD,点E为VA的中点.
如图,在四棱锥V-ABCD中,底面ABCD是正方形,侧棱VA⊥底面ABCD,点E为VA的中点.