题目内容
若向量
、
的坐标满
+
=(-2,-1,2),
-
=(4,-3,-2),则
•
的等于( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、5 | B、-5 | C、7 | D、-1 |
考点:空间向量的数量积运算
专题:空间向量及应用
分析:由已知求出向量
、
的坐标,然后利用数量积定义求之.
| a |
| b |
解答:
解:因为向量
、
的坐标满
+
=(-2,-1,2),
-
=(4,-3,-2),
所以向量
={1,-2,0}、
={-3,1,2},
所以
•
=-3-2+0=-5;
故选:B.
| a |
| b |
| a |
| b |
| a |
| b |
所以向量
| a |
| b |
所以
| a |
| b |
故选:B.
点评:本题考查了空间向量加减的坐标运算以及数量积的坐标运算,与平面向量的运算类似,属于基础题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
已知a是函数f(x)=3x-log
x的零点,若0<x0<a,则f(x0)的值满足( )
| 1 |
| 3 |
| A、f(x0)<0 |
| B、f(x0)>0 |
| C、f(x0)=0 |
| D、f(x0)的符号不确定 |
圆x2+y2-4x=0和圆x2+y2+2y=0的位置关系是( )
| A、相离 | B、外切 | C、相交 | D、内切 |
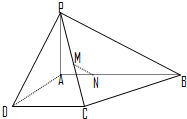 如图所示,在四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=DC=
如图所示,在四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=DC=