题目内容
经市场调查,某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t(天)的函数,且日销量近似满足g(t)=80-2t(件),当日价格近似满足f(t)=
(元).
(1)试写出该种商品的日销售额y与时间t(0≤t≤20)的函数表达式;
(2)求该种商品的日销售额y的最大值与最小值.
|
(1)试写出该种商品的日销售额y与时间t(0≤t≤20)的函数表达式;
(2)求该种商品的日销售额y的最大值与最小值.
考点:分段函数的应用
专题:函数的性质及应用
分析:(1)根据y=g(t)•f(t),可得该种商品的日销售额y与时间t(0≤t≤20)的函数表达式;
(2)分段求最值,可求该种商品的日销售额y的最大值.
(2)分段求最值,可求该种商品的日销售额y的最大值.
解答:
解:(1)该种商品的日销售额y与时间t(0≤t≤20)的函数表达式为:
y=g(t)•f(t)=
;
(2)当0≤t<10时,y=(30+t)(40-t)=-(t-5)2+1225,
∴y的取值范围是[1200,1225],在t=5时,y取得最大值为1225;
当10≤t≤20时,y=(50-t)(40-t)=(t-45)2-25,
∴y的取值范围是[600,1200],在t=10时,y取得最小值为1200.
∴第5天时,日销售额y取得最大,为1225元.
第10天时,日销售额y取得最小,为1200元.
y=g(t)•f(t)=
|
(2)当0≤t<10时,y=(30+t)(40-t)=-(t-5)2+1225,
∴y的取值范围是[1200,1225],在t=5时,y取得最大值为1225;
当10≤t≤20时,y=(50-t)(40-t)=(t-45)2-25,
∴y的取值范围是[600,1200],在t=10时,y取得最小值为1200.
∴第5天时,日销售额y取得最大,为1225元.
第10天时,日销售额y取得最小,为1200元.
点评:本题考查利用数学知识解决实际问题,考查函数最值的研究,考查学生的计算能力,利用二次函数的性质是解决本题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
下列说法错误的是( )
| A、如果命题“¬p”与命题“p或q”都是真命题,那么命题q一定是真命题 |
| B、命题“若a=0,则ab=0”的逆否命题是:“若a≠0,则ab≠0” |
| C、命题p:存在x∈R,使x2-2x+4<0,则¬p:对任意的x∈R,x2-2x+4≥0 |
| D、命题“存在x∈R,使-2x2+x-4=0”是真命题 |
若α,β,γ表示平面,m,n表示直线,则下列命题中,正确的是( )
| A、m?α,n?α,m∥β,n∥β,则α∥β |
| B、若α⊥γ,β⊥γ,则α∥β |
| C、若α∥β,m?α,n?β,则m∥n |
| D、若α∥β,m?α,则m∥β |
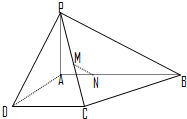 如图所示,在四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=DC=
如图所示,在四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=DC=