题目内容
已知f(
-1)=x-2
+2,则f(x)= .
| x |
| x |
考点:函数解析式的求解及常用方法
专题:配方法,换元法,函数的性质及应用
分析:用配方法,得出f(
-1)=(
-1)2+1,再设t=
-1,t≥-1;求出f(t)即可.
| x |
| x |
| x |
解答:
解:∵f(
-1)=x-2
+2
=(
)2-2
+1+1
=(
-1)2+1,
设t=
-1,t≥-1;
∴f(t)=t2+1,t≥-1;
即f(x)=x2+1,x∈[-1,+∞).
故答案为:x2+1,x∈[-1,+∞).
| x |
| x |
=(
| x |
| x |
=(
| x |
设t=
| x |
∴f(t)=t2+1,t≥-1;
即f(x)=x2+1,x∈[-1,+∞).
故答案为:x2+1,x∈[-1,+∞).
点评:本题考查了利用配方法与换元法求函数解析式的应用问题,是基础题目.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
设i是虚数单位,若复数
为纯虚数,则实数m的值为( )
| 2-mi |
| 1+i |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
函数f(x)=2x-tanx在(-
,
)上的图象大致是( )
| π |
| 2 |
| π |
| 2 |
A、 |
B、 |
C、 |
D、 |
实数x,y满足
,若t≤y+2x恒成立,则t的取值范围是( )
|
| A、t≤13 | B、t≤-5 |
| C、t≤-13 | D、t≤5 |
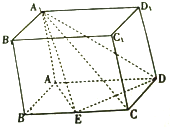 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AB=1,BC=2,∠ABC=60°,E为BC的中点,AA1⊥平面ABCD.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AB=1,BC=2,∠ABC=60°,E为BC的中点,AA1⊥平面ABCD.