题目内容
3.已知棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是棱B1C1,C1D1的中点.(I)求AD1与EF所成角的大小;
(II)求AF与平面BEB1所成角的余弦值.
分析 (I)建立如图所示的坐标系,利用向量法求AD1与EF所成角的大小;
(II)求出平面BEB1的法向量,利用向量法求AF与平面BEB1所成角的余弦值.
解答 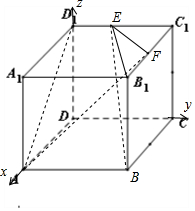 解:(I)建立如图所示的坐标系,D(0,0,0),A(1,0,0),
解:(I)建立如图所示的坐标系,D(0,0,0),A(1,0,0),
E(0,$\frac{1}{2}$,1),F($\frac{1}{2}$,1,1),D1(0,0,1),
$\overrightarrow{A{D}_{1}}$=(-1,0,1),$\overrightarrow{EF}$=($\frac{1}{2}$,$\frac{1}{2}$,0),
设AD1与EF所成角为α,∴cosα=|$\frac{-\frac{1}{2}}{\sqrt{2}•\sqrt{\frac{1}{4}+\frac{1}{4}}}$|=$\frac{1}{2}$,
∴AD1与EF所成角的大小为60°;
(II)$\overrightarrow{B{B}_{1}}$=(0,0,1),$\overrightarrow{BE}$=(-1,-$\frac{1}{2}$,1),
设平面BEB1的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{z=0}\\{-x-\frac{y}{2}+z=0}\end{array}\right.$,
取$\overrightarrow{n}$=(1,-2,0),
∵$\overrightarrow{AF}$=(-$\frac{1}{2}$,1,1),
∴AF与平面BEB1所成角的正弦值为|$\frac{-\frac{1}{2}-2}{\sqrt{5}•\sqrt{\frac{1}{4}+1+1}}$|=$\frac{\sqrt{5}}{3}$,
∴AF与平面BEB1所成角的余弦值为$\frac{2}{3}$.
点评 本题考查线线角,考查线面角,考查向量方法的运用,属于中档题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 109 | B. | 99 | C. | $\frac{99}{2}$ | D. | $\frac{109}{2}$ |
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{1}{2}$ |