题目内容

14．“a≤0”是“函数f（x）=ax+lnx存在极值”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

分析 根据函数极值和导数的关系，结合充分条件和必要条件的定义进行判断即可．

解答 解：函数f（x）的定义域为（0，+∞），函数的导数f′（x）=a+$\frac{1}{x}$，
若函数f（x）=ax+lnx存在极值，则f′（x）=0有解，即a+$\frac{1}{x}$=0，即a=-$\frac{1}{x}$，
∵x＞0，∴a=-$\frac{1}{x}$＜0，
则“a≤0”是“函数f（x）=ax+lnx存在极值”的必要不充分条件，
故选：B

点评 本题主要考查充分条件和必要条件的判断，根据函数极值和导数之间的关系求出a的取值范围是解决本题的关键．

练习册系列答案
相关题目
4．已知函数y=f（x）的图象关于直线x=1对称，当x＜1时，f（x）=|（$\frac{1}{2}$）x-1|，那么当x＞1时，函数f（x）的递增区间是（　　）
A．（-∞，0）B．（1，2）C．（2，+∞）D．（2，5）
5．若关于x的方程$\sqrt{-{x}^{2}+4x-3}$=mx+m-1有两个不同的实数根，则实数m的取值范围是（　　）
A．（0，$\frac{3}{4}$）B．[$\frac{1}{2}$，$\frac{3}{4}$）C．（$\frac{1}{4}$，$\frac{1}{2}$）D．[$\frac{1}{4}$，$\frac{3}{4}$）
2．已知抛物线C：y2=2px（p＞0）经过点（4，-4）．
（1）若抛物线C上一动点M到准线的距离为d，D（-1，3），求d+|MD|的最小值；
（2）若直线l与抛物线C交于A，B两点，且线段AB的中点为N（2，$\frac{1}{3}$），求直线l的方程．
9．若集合A={x∈N|5+4x-x2＞0}，B={x|x＜3}，则A∩B等于（　　）
A．∅B．{1，2}C．[0，3）D．{0，1，2}
19．设命题p：?x0∈（-2，+∞），6+|x0|=5，命题q：?x∈（-∞，0），x2+$\frac{4}{{x}^{2}}$≥4．命题r：若a≥1，则函数f（x）=ax+cosx（x∈R）是增函数．
（1）写出命题r的否命题；
（2）判断命题￢p：p∨r，p∧q的真假，并说明理由．
6．斜率为1的直线与抛物线y=ax2（a＞0）交于A、B两点，且线段AB的中点C到y轴的距离为1，则该抛物线焦点到准线的距离为（　　）
A．$\frac{1}{4}$B．$\frac{1}{2}$C．1D．2
3．已知棱长为1的正方体ABCD-A1B1C1D1中，E，F分别是棱B1C1，C1D1的中点．
（I）求AD1与EF所成角的大小；
（II）求AF与平面BEB1所成角的余弦值．
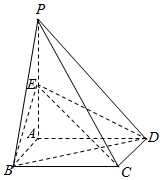4．如图，四棱锥P-ABCD的底面是正方形，侧棱PA⊥底面ABCD，E是PA的中点．
（Ⅰ）求证：PC∥平面BDE；
（Ⅱ）证明：BD⊥CE．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网