已知m＞0.10=a0+a1x+a2x2+-+a10x10.若a1+a2+-+a10=1023.则实数m=1．题目和参考答案——青夏教育精英家教网—

题目内容

6．已知m＞0，（1+mx）¹⁰=a₀+a₁x+a₂x²+…+a₁₀x¹⁰，若a₁+a₂+…+a₁₀=1023，则实数m=1．

分析由题意令x=0，求得a₀=1．再令x=1，结合a₁+a₂+…+a₁₀=1023，求得m的值．

解答解：∵m＞0，（1+mx）¹⁰=a₀+a₁x+a₂x²+…+a₁₀x¹⁰，故令x=0，可得a₀=1．
再令x=1，可得 a₀+a₁+a₂+…+a₁₀=1024=（1+m）¹⁰，∴m=1，
故答案为：1．

点评本题主要考查二项式定理的应用，是给变量赋值的问题，关键是根据要求的结果，选择合适的数值代入，属于基础题．

练习册系列答案

相关题目

16．已知如图所示的程序框图，则输出的结果是9．

17．

某小学对五年级的学生进行体质测试，已知五年级一班共有学生30人，测试立定跳远的成绩用茎叶图表示如下（单位：cm）：
男生成绩在175cm以上（包括175cm）定义为“合格”，成绩在175cm以下（不包括175cm）定义为“不合格”；
女生成绩在165cm以上（包括165cm）定义为“合格”，成绩在165cm以下（不包括165cm）定义为“不合格”
（Ⅰ）在五年级一班男生中任意选取3人，求至少有2人的成绩是合格的概率；
（Ⅱ）若从五年级一班成绩“合格”的学生中选取2人参加复试，用X表示其中男生的人数，写出X的分布列，并求X的数学期望．

14．已知i是虚数单位，则复数z=i（1-i）的实部为（　　）

1．2016年3月，韩国著名围棋棋手李世石与谷歌A1phaGo的人机大战赛在韩国首尔举行，比赛中采取五局分胜负的方式（即下完五局），获胜者将获得100万美元的奖励，假设在每局比赛中AlphaGo获胜的概率是$\frac{2}{3}$，李世石获胜的概率是$\frac{1}{3}$．
（I）求比赛结果为谷歌A1ph8Go以4：1获胜的概率；
（Ⅱ）若将比赛规则改为一方获得三局胜利后就赢得并结束比赛．设X表示比赛的局数，求X的分布列与数学期望．

11．

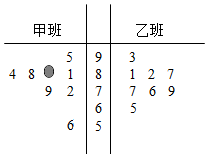为了解甲、乙两个班级（人数均为60人，入学数学平均分和优秀率都相同，学生勤奋程度和自觉性都一样）的数学成绩，现随机抽取甲、乙两个班级各8名同学的数学考试成绩，并做出茎叶图，但是不慎污损．已知两个班级所抽取的同学平均成绩相同，回答下面的问题并写出计算过程：
（I）求出甲班中被污损的一名学生的成绩；
（Ⅱ）样本中考试分数在70～90分之问的同学里，两班各任选一名同学座谈，甲乙两班被选出的两名同学分数均在80～90分的概率为多少．

18．已知集合S={x∈R|x+1≥2}，T={-2，-1，0，1，2}，则集合S∩T中元素的个数是（　　）

15．设数列{a_n}的前n项和S_n=n²+n，则a₄的值为（　　）

16．在等差数列{a_n}中，前11项和为S₁₁，若a₆+S₁₁=12，则a₂+a₅+a₇+a₁₀的和为（　　）

试题分类