题目内容
17. 某小学对五年级的学生进行体质测试,已知五年级一班共有学生30人,测试立定跳远的成绩用茎叶图表示如下(单位:cm):
某小学对五年级的学生进行体质测试,已知五年级一班共有学生30人,测试立定跳远的成绩用茎叶图表示如下(单位:cm):男生成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下(不包括175cm)定义为“不合格”;
女生成绩在165cm以上(包括165cm)定义为“合格”,成绩在165cm以下(不包括165cm)定义为“不合格”
(Ⅰ)在五年级一班男生中任意选取3人,求至少有2人的成绩是合格的概率;
(Ⅱ)若从五年级一班成绩“合格”的学生中选取2人参加复试,用X表示其中男生的人数,写出X的分布列,并求X的数学期望.
分析 (Ⅰ)设“仅有两人的成绩合格”为事件A,“有三人的成绩合格”为事件B,至少有两人的成绩是合格的概率为P=P(A)+P(B),由此能求出至少有2人的成绩是合格的概率.
(Ⅱ)因为女生共有18人,其中有10人合格,依题意,X的取值为0,1,2.分别求出相应的概率,由此能求出X的分布列和E(X).
解答 解:(Ⅰ)设“仅有两人的成绩合格”为事件A,“有三人的成绩合格”为事件B,
至少有两人的成绩是合格的概率为P,则P=P(A)+P(B),
又男生共12人,其中有8人合格,从而P(A)=$\frac{{C}_{4}^{1}•{C}_{8}^{2}}{{C}_{12}^{3}}$,…(2分)
P(B)=$\frac{{C}_{8}^{3}}{{C}_{12}^{3}}$,…(4分)所以P=$\frac{42}{55}$.…(6分)
(Ⅱ)因为女生共有18人,其中有10人合格,依题意,X的取值为0,1,2.
则P(X=0)=$\frac{{C}_{8}^{0}{C}_{10}^{2}}{{C}_{18}^{2}}$=$\frac{5}{17}$,P(X=1)=$\frac{{C}_{8}^{1}{C}_{10}^{1}}{{C}_{18}^{2}}$=$\frac{80}{153}$,
P(X=2)=$\frac{{C}_{8}^{2}{C}_{10}^{0}}{{C}_{18}^{2}}$=$\frac{28}{153}$,(每项1分) …(10分)
因此,X的分布列如下:
| X | 0 | 1 | 2 |
| P | $\frac{5}{17}$ | $\frac{80}{153}$ | $\frac{28}{153}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.“|x-1|<2成立”是“x(x-3)<0成立”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不不充分也不必要条件 |
8.某单位老年人、中年人、青年人的人数如表,用分层抽样的方法抽取17人进行单位管理问卷调查,其中抽到3位老年人,则抽到的中年人人数为( )
| 类别 | 人数 |
| 老年人 | 15 |
| 中年人 | ? |
| 青年人 | 40 |
| A. | 9 | B. | 8 | C. | 6 | D. | 3 |
5.如图所示的框图,若输入的n的值为4,则输出的S=( )
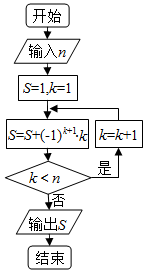

| A. | 3 | B. | 4 | C. | -1 | D. | 0 |
12.设数列{an}的前n项和为S,若Sn+1,Sn+2,Sn+3成等差数列,且a2=-2,则a7=( )
| A. | 16 | B. | 32 | C. | 64 | D. | 128 |
7.已知$\overrightarrow{a}$=(cos2x-sin2x,-$\sqrt{3}$),$\overrightarrow{b}$=(1,cos($\frac{π}{2}$+2x)),若f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$,则f(x)( )
| A. | 图象关于$({-\frac{π}{6},0})$中心对称 | B. | 图象关于直线$x=-\frac{π}{6}$对称 | ||
| C. | 在区间$[{-\frac{π}{6},0}]$上单调递增 | D. | 周期为π的奇函数 |