题目内容
已知函数f1(x)=e|x-2a+1|,f2(x)=e|x-a|+1,x∈R,1≤a≤6.
(1)若a=2,求使f1(x)=f2(x)的x的值;
(2)若|f1(x)-f2(x)|=f2(x)-f1(x)对于任意的实数x恒成立,求a的取值范围;
(3)求函数g(x)=
-
在[1,6]上的最小值.
(1)若a=2,求使f1(x)=f2(x)的x的值;
(2)若|f1(x)-f2(x)|=f2(x)-f1(x)对于任意的实数x恒成立,求a的取值范围;
(3)求函数g(x)=
| f1(x)+f2(x) |
| 2 |
| |f1(x)-f2(x)| |
| 2 |
考点:指数函数综合题,指数型复合函数的性质及应用
专题:函数的性质及应用
分析:(1)若a=2,解方程f1(x)=f2(x)即可求x的值;
(2)若|f1(x)-f2(x)|=f2(x)-f1(x)对于任意的实数x恒成立,转化为f1(x)≤f2(x)恒成立,即可求a的取值范围;
(3)求出g(x)的表达式,讨论a的取值范围即可求出函数的最值.
(2)若|f1(x)-f2(x)|=f2(x)-f1(x)对于任意的实数x恒成立,转化为f1(x)≤f2(x)恒成立,即可求a的取值范围;
(3)求出g(x)的表达式,讨论a的取值范围即可求出函数的最值.
解答:
 解:(1)若a=2,则f1(x)=e|x-3|,f2(x)=e|x-2|+1,
解:(1)若a=2,则f1(x)=e|x-3|,f2(x)=e|x-2|+1,
由f1(x)=f2(x)得e|x-3|=e|x-2|+1,
即|x-3|=|x-2|+1,
若x≥3,则方程等价为x-3=x-2+1,即-3=-1,不成立,
若2<x<3,则方程等价为-x+3=x-2+1,即2x=4,解得x=2,不成立,
若x<2,则方程等价为-x+3=-x+2+1,此时恒成立;
综上使f1(x)=f2(x)的x的值满足x<2.
(2)即f1(x)≤f2(x)恒成立,得|x-2a+1|≤|x-a|+1,
即|x-2a+1|-|x-a|≤1对x∈R恒成立,
因|x-2a+1|-|x-a|≤|a-1|,
故只需|a-1|≤1,解得0≤a≤2,
又1≤a≤6,
故a的取值范围为1≤a≤2.
(3)g(x)=
①当1≤a≤2时,由(2)知g(x)=f1(x)=e|x-2a+1|,
当x=2a-1∈[1,3]时,g(x)min=1.
②当2<a≤6时,(2a-1)-a=a-1>0,
故2a-1>a.x≤a时,f1(x)=e-x+(2a-1)>e-x+a+1=f2(x),g(x)=f2(x)=e|x-a|+1;
x≥2a-1时,f1(x)=ex-(2a-1)<ex-a+1=f2(x),g(x)=f1(x)=e|x-2a+1|;
a<x<2a-1时,由f1(x)=e-x+(2a-1)≤ex-a+1=f2(x),得x≥
,其中a<
<2a-1,
故当
≤x<2a-1时,g(x)=f1(x)=e|x-2a+1|;
当a<x<
时,g(x)=f2(x)=e|x-a|+1.
因此,当2<a≤6时,g(x)=
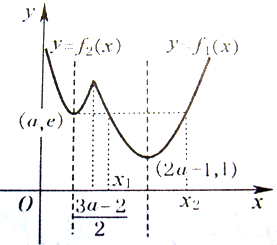
令f1(x)=e|x-2a+1|=e,得x1=2a-2,x2=2a,且
<2a-2,如图,
(ⅰ)当a≤6≤2a-2,即4≤a≤6时,g(x)min=f2(a)=e;
(ⅱ) 当2a-2<6≤2a-1,即
≤a<4时,g(x)min=f1(6)=e2a-7;
(ⅲ) 当2a-1<6,即2<a<
时,g(x)min=f1(2a-1)=1.
综上所述,g(x)min=
.
 解:(1)若a=2,则f1(x)=e|x-3|,f2(x)=e|x-2|+1,
解:(1)若a=2,则f1(x)=e|x-3|,f2(x)=e|x-2|+1,由f1(x)=f2(x)得e|x-3|=e|x-2|+1,
即|x-3|=|x-2|+1,
若x≥3,则方程等价为x-3=x-2+1,即-3=-1,不成立,
若2<x<3,则方程等价为-x+3=x-2+1,即2x=4,解得x=2,不成立,
若x<2,则方程等价为-x+3=-x+2+1,此时恒成立;
综上使f1(x)=f2(x)的x的值满足x<2.
(2)即f1(x)≤f2(x)恒成立,得|x-2a+1|≤|x-a|+1,
即|x-2a+1|-|x-a|≤1对x∈R恒成立,
因|x-2a+1|-|x-a|≤|a-1|,
故只需|a-1|≤1,解得0≤a≤2,
又1≤a≤6,
故a的取值范围为1≤a≤2.
(3)g(x)=
|
①当1≤a≤2时,由(2)知g(x)=f1(x)=e|x-2a+1|,
当x=2a-1∈[1,3]时,g(x)min=1.
②当2<a≤6时,(2a-1)-a=a-1>0,
故2a-1>a.x≤a时,f1(x)=e-x+(2a-1)>e-x+a+1=f2(x),g(x)=f2(x)=e|x-a|+1;
x≥2a-1时,f1(x)=ex-(2a-1)<ex-a+1=f2(x),g(x)=f1(x)=e|x-2a+1|;
a<x<2a-1时,由f1(x)=e-x+(2a-1)≤ex-a+1=f2(x),得x≥
| 3a-2 |
| 2 |
| 3a-2 |
| 2 |
故当
| 3a-2 |
| 2 |
当a<x<
| 3a-2 |
| 2 |
因此,当2<a≤6时,g(x)=
|
令f1(x)=e|x-2a+1|=e,得x1=2a-2,x2=2a,且
| 3a-2 |
| 2 |
(ⅰ)当a≤6≤2a-2,即4≤a≤6时,g(x)min=f2(a)=e;
(ⅱ) 当2a-2<6≤2a-1,即
| 7 |
| 2 |
(ⅲ) 当2a-1<6,即2<a<
| 7 |
| 2 |
综上所述,g(x)min=
|
点评:本题主要考查函数性质的应用,利用指数函数的图象和性质是解决本题的关键.综合性较强,运算量较大,有一定的难度.

练习册系列答案
相关题目
空间直角坐标系中已知点P(0,0,
)和点C(-1,2,0),则在y上到P,C的距离相等的点M的坐标是( )
| 3 |
| A、(0,1,0) | ||
B、(0,
| ||
C、(0,-
| ||
| D、(0,2,0) |
与直线l:3x-4y-1=0平行且到直线l的距离为2的直线方程是( )
| A、3x-4y-11=0或3x-4y+9=0 |
| B、3x-4y-11=0 |
| C、3x-4y+11=0或3x-4y-9=0 |
| D、3x-4y+9=0 |
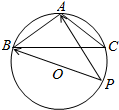 如图,在△ABC中,三内角A,B,C的对边分别为a,b,c,且a2=b2+c2+bc,a=
如图,在△ABC中,三内角A,B,C的对边分别为a,b,c,且a2=b2+c2+bc,a=