题目内容
给出下列四个命题:
①若x>0,且x≠1则lgx+
≥2;
②设x,y∈R,命题“若xy=0,则x2+y2=0”的否命题是真命题;
③函数y=cos(2x-
)的一条对称轴是直线x=
π;
④若定义在R上的函数y=f(x)是奇函数,则对定义域内的任意x必有f(2x+1)+f(-2x-1)=0.
其中,所有正确命题的序号是 .
①若x>0,且x≠1则lgx+
| 1 |
| lgx |
②设x,y∈R,命题“若xy=0,则x2+y2=0”的否命题是真命题;
③函数y=cos(2x-
| π |
| 3 |
| 5 |
| 12 |
④若定义在R上的函数y=f(x)是奇函数,则对定义域内的任意x必有f(2x+1)+f(-2x-1)=0.
其中,所有正确命题的序号是
考点:命题的真假判断与应用
专题:简易逻辑
分析:求出当0<x<1时lgx+
的范围判断①;判断原命题的逆命题的真假,从而得到原命题的否命题的真假判断②;把x=
π代入函数y=cos(2x-
)求得函数值判断③;
由奇函数的概念结合自变量的任意性判断④.
| 1 |
| lgx |
| 5 |
| 12 |
| π |
| 3 |
由奇函数的概念结合自变量的任意性判断④.
解答:
解:对于①,当0<x<1时,lgx<0,则lgx+
≤-2,命题①错误;
对于②,设x,y∈R,命题“若xy=0,则x2+y2=0”的逆命题为“若x2+y2=0,则xy=0”,为真命题,则其否命题也为真命题,命题②是真命题;
对于③,∵cos(2×
-
)=cos
=0,∴函数y=cos(2x-
)的一条对称轴是直线x=
π为假命题;
对于④,若定义在R上的函数y=f(x)是奇函数,则对定义域内的任意x必有f(x)+f(-x)=0,取x为2x+1,则f(2x+1)+f(-2x-1)=0,命题④正确.
故答案为:②④.
| 1 |
| lgx |
对于②,设x,y∈R,命题“若xy=0,则x2+y2=0”的逆命题为“若x2+y2=0,则xy=0”,为真命题,则其否命题也为真命题,命题②是真命题;
对于③,∵cos(2×
| 5π |
| 12 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| 5 |
| 12 |
对于④,若定义在R上的函数y=f(x)是奇函数,则对定义域内的任意x必有f(x)+f(-x)=0,取x为2x+1,则f(2x+1)+f(-2x-1)=0,命题④正确.
故答案为:②④.
点评:本题考查了命题的真假判断与应用,考查了函数的性质,对于④的周期理解是解答该题的关键,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果数据x1,x2,x3,…xn的平均数为
,方差为s2,则:数据3x1+5,3x2+5,3x3+5,…3xn+5的平均数和方差分别是( )
. |
| x |
A、
| ||
B、3
| ||
C、3
| ||
D、3
|
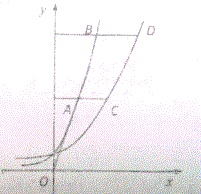 如图,A,B是函数y=e2x的图象上两点,分别过A B作x轴的平行线与函数y=ex的图象交于C,D两点.
如图,A,B是函数y=e2x的图象上两点,分别过A B作x轴的平行线与函数y=ex的图象交于C,D两点.