题目内容
已知tanα=2,求2sinαcosα-3cos2α的值.
考点:同角三角函数基本关系的运用
专题:计算题,三角函数的求值
分析:由二倍角公式化简后,用万能公式化简代入已知即可求值.
解答:
解:∵tanα=2,
∴2sinαcosα-3cos2α=sin2α-
-
cos2α=
-
-
×
=
-
-
×
=
.
∴2sinαcosα-3cos2α=sin2α-
| 3 |
| 2 |
| 3 |
| 2 |
| 2tanα |
| 1+tan2α |
| 3 |
| 2 |
| 3 |
| 2 |
| 1-tan2α |
| 1+tan2α |
| 4 |
| 5 |
| 3 |
| 2 |
| 3 |
| 2 |
| (-3) |
| 5 |
| 1 |
| 5 |
点评:本题主要考查了二倍角公式,万能公式的应用,属于基本知识的考查.

练习册系列答案
相关题目
下列各组中,两个集合相等的是( )
| A、M={(1,2)},N={(2,1)} | ||
| B、M={1,2},N={(1,2)} | ||
| C、M={x|x=2k+1,k∈Z},N={x|x=2k-1,k∈Z} | ||
D、M={(x,y)|
|
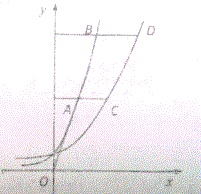 如图,A,B是函数y=e2x的图象上两点,分别过A B作x轴的平行线与函数y=ex的图象交于C,D两点.
如图,A,B是函数y=e2x的图象上两点,分别过A B作x轴的平行线与函数y=ex的图象交于C,D两点. 给出数表:请在其中找出5个不同的数,使它们由小到大能构成等比数列,则这5个数依次可以说是
给出数表:请在其中找出5个不同的数,使它们由小到大能构成等比数列,则这5个数依次可以说是