题目内容
下列函数f(x)中,满足“对任意的x1,x2∈(0,+∞),当x1<x2时,都有f(x1)<f(x2)”的是( )
A、f(x)=log
| ||
| B、f(x)=sinx | ||
| C、f(x)=x3 | ||
| D、f(x)=e-x |
考点:函数单调性的判断与证明,函数单调性的性质
专题:函数的性质及应用
分析:根据增函数的定义,由已知条件即可得到f(x)在(0,+∞)上是增函数,所以根据对数函数、正弦函数、幂函数、指数函数的单调性即可找出正确选项.
解答:
解:根据已知条件及增函数的定义知f(x)在(0,+∞)上是增函数;
A.f(x)=log
(x+1)在(0,+∞)上为减函数;
B.f(x)=sinx在(0,+∞)上没有单调性;
C.根据f(x)=x3的图象知该函数在(0,+∞)上为增函数,所以该选项正确;
D.f(x)=e-x,根据单调性的定义及指数函数的单调性知该函数在(0,+∞)上为减函数.
故选C.
A.f(x)=log
| 1 |
| 2 |
B.f(x)=sinx在(0,+∞)上没有单调性;
C.根据f(x)=x3的图象知该函数在(0,+∞)上为增函数,所以该选项正确;
D.f(x)=e-x,根据单调性的定义及指数函数的单调性知该函数在(0,+∞)上为减函数.
故选C.
点评:考查函数单调性的定义,以及对数函数,正弦函数,幂函数,以及指数函数的单调性.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
若函数y=f(x)是函数y=ax(a>0,且a≠1)的反函数,其图象经过点(2,1),则f(x)=( )
| A、log2x | ||
B、log
| ||
C、
| ||
| D、x2 |
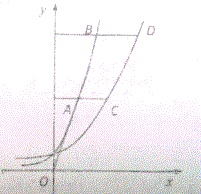 如图,A,B是函数y=e2x的图象上两点,分别过A B作x轴的平行线与函数y=ex的图象交于C,D两点.
如图,A,B是函数y=e2x的图象上两点,分别过A B作x轴的平行线与函数y=ex的图象交于C,D两点.