题目内容
已知直线l垂直于直线2x-3y+5=0,则直线l的一个法向量
= .
| n |
考点:直线的一般式方程与直线的垂直关系
专题:平面向量及应用,直线与圆
分析:由直线方程及直线垂直求得直线l的斜率,则直线l的法向量可求.
解答:
解:∵直线2x-3y+5=0的斜率为
,且直线l垂直直线2x-3y+5=0,
∴l的一个法向量为(1,
)=
(3,2),
故答案为:(3,2).
| 2 |
| 3 |
∴l的一个法向量为(1,
| 2 |
| 3 |
| 1 |
| 3 |
故答案为:(3,2).
点评:本题考查了直线的一般式方程与直线垂直间的关系,考查了直线的方向向量和法向量,是基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
某程序框图如图所示,则该程序运行后输出的S的值等于( )


| A、1 | ||
B、
| ||
C、
| ||
D、
|
一个几何体的三视图如图所示,则该几何体的体积等于( )


A、
| ||
B、
| ||
C、
| ||
| D、1 |
已知函数f(x)=
,则下列说法正确的是( )
| x-1 |
| x+2 |
| A、f(x)在R上为增函数 |
| B、f(x)在(-∞,-2)上为减函数,在(-2,+∞)上也为减函数 |
| C、f(x)在(-∞,-2)上为减函数,在(-2,+∞)上为增函数 |
| D、f(x)在(-∞,-2)上为增函数,在(-2,+∞)上为增函数 |
下列各组中,两个集合相等的是( )
| A、M={(1,2)},N={(2,1)} | ||
| B、M={1,2},N={(1,2)} | ||
| C、M={x|x=2k+1,k∈Z},N={x|x=2k-1,k∈Z} | ||
D、M={(x,y)|
|
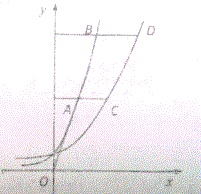 如图,A,B是函数y=e2x的图象上两点,分别过A B作x轴的平行线与函数y=ex的图象交于C,D两点.
如图,A,B是函数y=e2x的图象上两点,分别过A B作x轴的平行线与函数y=ex的图象交于C,D两点.