题目内容
等差数列{αn}的前n项和Sn=
n2,数列{βn}满足βn=
.同学甲在研究性学习中发现以下六个等式均成立:
①sin2α1+cos2β1-sinα1cosβ1=m; ②sin2α2+cos2β2-sinα2cosβ2=m;
③sin2α3+cos2β3-sinα3cosβ3=m;④sin2α4+cos2β4-sinα4cosβ4=m;
⑤sin2α5+cos2β5-sinα5cosβ5=m;⑥sin2α6+cos2β6-sinα6cosβ6=m.
(Ⅰ)求数列{αn}的通项公式;
(Ⅱ)试从上述六个等式中选择一个,求实数m的值;
(Ⅲ)根据(Ⅱ)的计算结果,将同学甲的发现推广为三角恒等式,并证明你的结论.
| π |
| 36 |
| (7-2n)π |
| 36 |
①sin2α1+cos2β1-sinα1cosβ1=m; ②sin2α2+cos2β2-sinα2cosβ2=m;
③sin2α3+cos2β3-sinα3cosβ3=m;④sin2α4+cos2β4-sinα4cosβ4=m;
⑤sin2α5+cos2β5-sinα5cosβ5=m;⑥sin2α6+cos2β6-sinα6cosβ6=m.
(Ⅰ)求数列{αn}的通项公式;
(Ⅱ)试从上述六个等式中选择一个,求实数m的值;
(Ⅲ)根据(Ⅱ)的计算结果,将同学甲的发现推广为三角恒等式,并证明你的结论.
考点:三角函数的化简求值,归纳推理
专题:三角函数的求值,推理和证明
分析:(Ⅰ)利用等差数列{αn}的前n项和Sn=
n2,分n=1与n≥2讨论,即可求得数列{αn}的通项公式;
(Ⅱ)选择②,计算即可;
(Ⅲ)利用两角差的余弦将所求关系式中的cos2(
-θ)及cos(
-θ)展开,利用平方关系计算即可证得结论成立.
| π |
| 36 |
(Ⅱ)选择②,计算即可;
(Ⅲ)利用两角差的余弦将所求关系式中的cos2(
| π |
| 6 |
| π |
| 6 |
解答:
(Ⅰ)解:当n=1时,α1=
…(1分)
当n≥2时,αn=Sn-Sn-1=
n2-
(n-1)2=
n-
…(3分)
∵当n=1时,a1适合此式∴数列{αn}的通项公式为an=
n-
…(5分)
(Ⅱ)解:选择②,计算如下:β2=
…(6分)
m=sin2α2+cos2β2-sinα2cosβ2
=sin2
+cos2
-sin
cos
=1-
sin
=
…(8分)
(Ⅲ)证明:sin2θ+cos2(
-θ)-sinθcos(
-θ)…(9分)
=sin2θ+(cos
cosθ+sin
sinθ)2-sinθ(cos
cosθ+sin
sinθ)…(10分)
=sin2θ+
cos2θ+
sin2θ+
sinθcosθ-
sinθcosθ-
sin2θ…(11分)
=
cos2θ+
sin2θ=
…(12分)
| π |
| 36 |
当n≥2时,αn=Sn-Sn-1=
| π |
| 36 |
| π |
| 36 |
| π |
| 18 |
| π |
| 36 |
∵当n=1时,a1适合此式∴数列{αn}的通项公式为an=
| π |
| 18 |
| π |
| 36 |
(Ⅱ)解:选择②,计算如下:β2=
| π |
| 12 |
m=sin2α2+cos2β2-sinα2cosβ2
=sin2
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
=1-
| 1 |
| 2 |
| π |
| 6 |
| 3 |
| 4 |
(Ⅲ)证明:sin2θ+cos2(
| π |
| 6 |
| π |
| 6 |
=sin2θ+(cos
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
=sin2θ+
| 3 |
| 4 |
| 1 |
| 4 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
点评:本题考查归纳推理,着重考查三角函数的化简求值,考查运算与推理证明能力,属于难题.

练习册系列答案
相关题目
已知函数f(x)=
,则f(-1)=( )
|
| A、0 | B、2 | C、4 | D、8 |
复数z=
(i是虚数单位)在复平面内对应的点位于( )
| 5 |
| 1+2i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
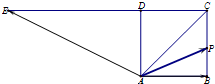 如图,四边形ABCD是边长为1的正方形,延长CD至E,使得DE=2CD.动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,
如图,四边形ABCD是边长为1的正方形,延长CD至E,使得DE=2CD.动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,