题目内容
5．小强和小华两位同学约定下午在大良钟楼公园喷水池旁见面，约定谁先到后必须等10分钟，这时若另一人还没有来就可以离开．如果小强是1：40-2：00到达的，假设小华在1点到2点内到达，且小华在 1点到2点之间何时到达是等可能的，则他们会面的概率是$\frac{17}{24}$．分析 由题意知本题是一个几何概型，以面积为测度，根据面积之比得到概率．
解答 解：由题意知本题是一个几何概型，
∵试验发生包含的所有事件对应的集合是Ω={x|100＜x＜120，60＜y＜120}，
集合对应的面积是1200，
而满足条件的事件={x|100＜x＜120，60＜y＜120，|x-y|≤10}，
对应的面积为$\frac{1}{2}×10×10+\frac{（30+50）×20}{2}$=850
∴两人能够会面的概率是$\frac{850}{1200}$=$\frac{17}{24}$，
故答案为$\frac{17}{24}$．
点评 本题主要考查几何概型的概率的计算，利用面积为测度是解决本题的关键．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
相关题目
15．已知直线y=$\frac{2\sqrt{5}}{5}$x与双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）交于A、B两点，若在双曲线上存在点P，使得|PA|=|PB|=$\frac{\sqrt{3}}{2}$|AB|，则双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | $\sqrt{5}$ |
20．
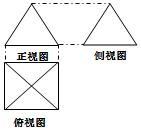如果一个几何体的三视图如图所示，正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形，（单位长度：cm），则此几何体的侧面积是（ ）
如果一个几何体的三视图如图所示，正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形，（单位长度：cm），则此几何体的侧面积是（ ）| A． | .$2\sqrt{3}$cm | B． | .$4\sqrt{3}$cm2 | C． | 8 cm2 | D． | 12 cm2 |
10．设Sn是等比数列{an}的前n项和为S4=4S2，则$\frac{{a}_{3}{a}_{8}}{{{a}_{5}}^{2}}$ 的值为（ ）
| A． | -2或-1 | B． | 1或2 | C． | ±$\sqrt{3}$或-1 | D． | ±1或2 |
17．某电脑公司有6名产品推销员，其工作年限与年推销金额的数据如表：
（1）以工作年限为自变量，推销金额为因变量y，作出散点图；
（2）求年推销金额y关于工作年限x的线性回归方程；
（3）若第6名推销员的工作年限为11年，试估计他的年推销金额．
附：回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中，$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{5}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{5}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x/年 | 3 | 5 | 6 | 7 | 9 |
| 推销金额y/万元 | 2 | 3 | 3 | 4 | 5 |
（2）求年推销金额y关于工作年限x的线性回归方程；
（3）若第6名推销员的工作年限为11年，试估计他的年推销金额．
附：回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中，$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{5}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{5}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．
15．在《增删算法统宗》中有这样一则故事：“三百七十八里关，初行健步不为难；次日脚痛减一半，六朝才得到其关．”意思是某人要走三百七八里的路程，第一天脚步轻快有力，走了一段路程，第二天脚痛，走的路程是第一天的一半，以后每天走的路程都是前一天的一半，走了六天才走完这段路程．则下列说法错误的是（ ）
| A． | 此人第二天走了九十六里路 | |
| B． | 此人第一天走的路程比后五天走的路程多六里 | |
| C． | 此人第三天走的路程占全程的$\frac{1}{8}$ | |
| D． | 此人后三天共走了42里路 |