题目内容
17.某电脑公司有6名产品推销员,其工作年限与年推销金额的数据如表:| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x/年 | 3 | 5 | 6 | 7 | 9 |
| 推销金额y/万元 | 2 | 3 | 3 | 4 | 5 |
(2)求年推销金额y关于工作年限x的线性回归方程;
(3)若第6名推销员的工作年限为11年,试估计他的年推销金额.
附:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{5}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{5}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
分析 (1)根据表中所给的5组数据,写出5个有序数对,画出平面直角坐标系,在坐标系中描出5个点,就是我们要求的散点图.
(2)首先求出x,y的平均数,利用最小二乘法做出b的值,再利用样本中心点满足线性回归方程和前面做出的横标和纵标的平均值,求出a的值,写出线性回归方程.
(3)第6名推销员的工作年限为11年,即当x=11时,把自变量的值代入线性回归方程,得到y的预报值,即估计出第6名推销员的年推销金额为5.9万元.
解答 解:(1)依题意,画出散点图如图所示,
(2)从散点图可以看出,这些点大致在一条直线附近,$\overline{x}$=6,$\overline{y}$=3.4,
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{5}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{5}({x}_{i}-\overline{x})^{2}}$=$\frac{10}{20}$=0.5,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=0.4,
∴年推销金额y关于工作年限x的线性回归方程为$\stackrel{∧}{y}$=0.5x+0.4.
(3)由(2)可知,当x=11时,
$\stackrel{∧}{y}$=0.5x+0.4=0.5×11+0.4=5.9(万元).
∴可以估计第6名推销员的年销售金额为5.9万元.
点评 本题考查回归分析的初步应用,考查利用最小二乘法求线性回归方程,是一个综合题目,这种题目非常符合新课标对于回归分析这一知识点的要求和考查思路.

练习册系列答案
相关题目
8.已知几何体的三视图如图所示,则该几何体的表面积是( )
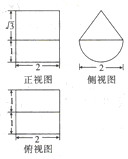

| A. | $2π+16+2\sqrt{3}$ | B. | $3π+16+2\sqrt{3}$ | C. | $3π+8+\sqrt{3}$ | D. | $3π+8+2\sqrt{3}$ |
12.执行如图所示的程序框图,则输出的结果为( )


| A. | 12 | B. | 11 | C. | 10 | D. | 9 |
7.若a=($\frac{1}{2}$)10,b=($\frac{1}{5}$)${\;}^{-\frac{1}{2}}$,c=log${\;}_{\frac{1}{3}}$10,则a,b.c大小关系为( )
| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | b>a>c |
 在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别边AB,BC上的点,且$\frac{CF}{FB}$=$\frac{AE}{EB}$=$\frac{1}{3}$.求证:
在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别边AB,BC上的点,且$\frac{CF}{FB}$=$\frac{AE}{EB}$=$\frac{1}{3}$.求证: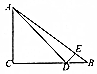 如图,在△ABC中,角A,B,C的对边分别为a,b,c,C=$\frac{π}{2}$,D,E分别为BC,AB上的点,∠ADC=∠EDB=$\frac{π}{4}$,DB=$\sqrt{2}$,AE=3EB,则边长AC的值为$\frac{3\sqrt{2}}{2}$.
如图,在△ABC中,角A,B,C的对边分别为a,b,c,C=$\frac{π}{2}$,D,E分别为BC,AB上的点,∠ADC=∠EDB=$\frac{π}{4}$,DB=$\sqrt{2}$,AE=3EB,则边长AC的值为$\frac{3\sqrt{2}}{2}$.