题目内容
已知函数f(x)=5-2|x|,g(x)=x2-2x,F(x)=
,则F(x)的最值为( )
|
A、最大值为5-2
| ||
B、最大值为5-2
| ||
| C、最大值为3,无最小值 | ||
| D、既无最大值,又无最小值 |
考点:分段函数的应用
专题:计算题,数形结合,函数的性质及应用
分析:根据F(x)的定义求出函数F(x)的表达式,利用数形结合即可求出函数的最值.
解答:
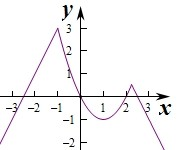 解:由f(x)=g(x)得5-2|x|=x2-2x,
解:由f(x)=g(x)得5-2|x|=x2-2x,
若x≥0时,5-2|x|=x2-2x等价为5-2x=x2-2x,
即x2=5,解得x=
.
若x<0时,5-2|x|=x2-2x等价为5+2x=x2-2x,
即x2-4x-5=0,
解得x=-1或x=5(舍去).
即当x≤-1时,F(x)=f(x)=5+2x,
当-1<x<
时,F(x)=g(x)=x2-2x,
当x≥
时,F(x)=f(x)=5-2x,
则由图象可知当x=-1时,F(x)取得最大值F(-1)=f(-1)=5-2=3,无最小值.
故选C.
 解:由f(x)=g(x)得5-2|x|=x2-2x,
解:由f(x)=g(x)得5-2|x|=x2-2x,若x≥0时,5-2|x|=x2-2x等价为5-2x=x2-2x,
即x2=5,解得x=
| 5 |
若x<0时,5-2|x|=x2-2x等价为5+2x=x2-2x,
即x2-4x-5=0,
解得x=-1或x=5(舍去).
即当x≤-1时,F(x)=f(x)=5+2x,
当-1<x<
| 5 |
当x≥
| 5 |
则由图象可知当x=-1时,F(x)取得最大值F(-1)=f(-1)=5-2=3,无最小值.
故选C.
点评:本题考查分段函数及运用,主要考查函数最值的求法,利用数形结合是解决本题的基本数学思想.

练习册系列答案
相关题目
已知集合A={x|2x-1≤0},B={x|x-a<0}.若A∩B=A,则实数a的取值范围( )
A、(
| ||
B、(-∞,
| ||
C、[
| ||
D、(-∞,
|
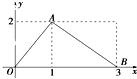 函数f(x)的图象是如下图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0)
函数f(x)的图象是如下图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0)