题目内容
求下列函数的导数:
(1)y=ax4-π2+2
(2)y=
+log2x
(3)y=
(4)y=2xtanx.
(1)y=ax4-π2+2
(2)y=
| 3 | x2 |
(3)y=
2x3-3x+
| ||
x
|
(4)y=2xtanx.
考点:导数的运算
专题:导数的概念及应用
分析:根据导数的运算法则即可得到结论.
解答:
解:(1)y′=4ax3,
(2)y=
+log2x=x
+log2x,则y′=
x-
+
.
(3)y=
=
-
+
-
=2x
-3x -
+x-1-x-
,
则y′=3x
+
x-
-x-2+
x-
.
(4)y=2xtanx=
,则y′=
=
.
(2)y=
| 3 | x2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| xln2 |
(3)y=
2x3-3x+
| ||
x
|
| 2x2 | ||
|
| 3 | ||
|
| 1 |
| x |
| 1 | ||
x
|
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
则y′=3x
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
(4)y=2xtanx=
| 2xsinx |
| cosx |
| (2xsinx)′-2xsinx(cosx)′ |
| cos2x |
| 2sinx+2xcosx+2xsin2x |
| cos2x |
点评:本题主要考查导数的计算,利用导数的运算法则是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 三棱锥P-ABC中,PC、AC、BC两两垂直,BC=PC=1,AC=2,E、F、G分别是AB、AC、AP的中点.
三棱锥P-ABC中,PC、AC、BC两两垂直,BC=PC=1,AC=2,E、F、G分别是AB、AC、AP的中点.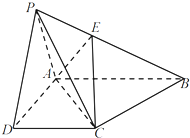 如图,四棱锥P-ABCD的底面是直角梯形,其中AB⊥AD,DC⊥AD,AB=AD=2,DC=1.侧面正△PAD所在平面与底面垂直.
如图,四棱锥P-ABCD的底面是直角梯形,其中AB⊥AD,DC⊥AD,AB=AD=2,DC=1.侧面正△PAD所在平面与底面垂直.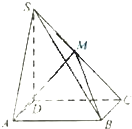 如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=
如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=