题目内容
设全集U={2，4，6，8}，A={4，6}，B={2，4，8}，则A∩（∁UB）=（ ）
| A、{6} | B、{4，6} |
| C、{2，6，8} | D、∅ |
考点：交、并、补集的混合运算
专题：集合
分析：根据全集U与B，求出B的补集，找出A与B补集的交集即可．
解答：
解：∵全集U={2，4，6，8}，A={4，6}，B={2，4，8}，
∴∁UB={6}，
则A∩（∁UB）={6}．
故选：A．
∴∁UB={6}，
则A∩（∁UB）={6}．
故选：A．
点评：此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
若函数f（x）=e-x+ax，x∈R有大于零的极值点，则实数a的取值范围为（ ）
| A、a＜1 | B、0＜a＜1 |
| C、-1＜a＜0 | D、a＜-1 |
如图所示程序运行后，输出的值是（ ）
| A、42 | B、43 | C、45 | D、44 |
已知函数f（x）=aln（x+1）-x2，在区间（-1，0）内任取两个实数p，q，且p≠q，若不等式
＞1恒成立，则实数a的取值范围为（ ）
| f(p+1)-f(q+1) |
| p-q |
| A、[6，+∞） | ||
| B、[4，+∞） | ||
C、[-
| ||
| D、[1，+∞） |
若定义在[-a，a]上的奇函数f（x）同时也是减函数，则函数y=f（-x）在[-a，a]上（ ）
| A、既是奇函数又是增函数 |
| B、既是奇函数又是减函数 |
| C、是偶函数且先增后减 |
| D、是偶函数且先减后增 |
等比数列{an}的前n项和为Sn，已知S1，2S2，3S3成等差数列，则数列{an}的公比为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示的圆盘由八个全等的扇形构成，指针绕中心旋转，可能随机停止则指针停止在阴影部分内的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
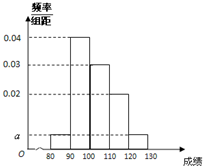为了分析我校市二模文科数学的成绩，现抽样统计了20位同学的数学成绩，形成了如图所示的频率分布直方图，其中成绩的分组区间是：[80，90），[90，100），[100，110），[110，120），[120，130]