题目内容
10.对于定义域为D的函数y=f(x),如果存在区间[m,n]⊆D(m<n),同时满足:①f(x)在[m,n]内是单调函数;②当定义域是[m,n]时,f(x)的值域也是[m,n]则称函数f(x)是区间[m,n]上的“保值函数”.(1)求证:函数g(x)=x2-2x不是定义域[0,1]上的“保值函数”;
(2)已知f(x)=2+$\frac{1}{a}$-$\frac{1}{{a}^{2}x}$(a∈R,a≠0)是区间[m,n]上的“保值函数”,求a的取值范围.
分析 (1)根据函数单调性的定义以及“保值函数”的定义判断即可;
(2)由f(x)的定义域和值域都是[m,n],问题等价于方程a2x2-(2a2+a)x+1=0有两个不等的实数根,根据根的判别式判断即可;
解答 解:(1)证明:g(x)=x2-2x=(x-1)2-1,
x∈[0,1]时,g(x)∈[-1,0],
根据函数g(x)不是定义域[0,1]上的“保值函数”.
(2))由f(x)的定义域和值域都是[m,n]得f(m)=m,f(n)=n,
因此m,n是方程2+$\frac{1}{a}$-$\frac{1}{{a}^{2}x}$=x的两个不相等的实数根,
等价于方程a2x2-(2a2+a)x+1=0有两个不等的实数根,
即△=(2a2+a)2-4a2>0,
解得a>$\frac{1}{2}$或a<-$\frac{3}{2}$.
点评 本题主要考查了函数单调性的判断与证明,以及函数恒成立问题,同时考查了转化与划归的思想,属于综合题.

练习册系列答案
相关题目
1.执行如图的程序框图,则输出S的值是( )


| A. | log47 | B. | log23 | C. | $\frac{3}{2}$ | D. | 2 |
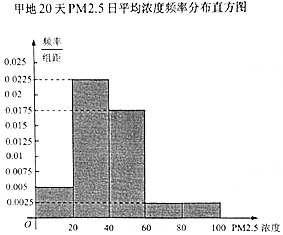
18.为检测空气质量,某市环保局随机抽取了甲、乙两地2016年20天PM2.5日平均浓度(单位:微克/立方米)监测数据,得到甲地PM2.5日平均浓度频率分布直方图和乙地PM2.5日平均浓度的频数分布表.
乙地20天PM2.5日平均浓度频数分布表
(1)根据乙地20天PM2.5日平均浓度的频率分布表,作出作出相应的频率分组直方图,并通过两个频率分布直方图比较两地PM2.5日平均浓度的平均值及分散程度(不要求计算出具体值,给出结论即可);
(2)通过调查,该市市民对空气质量的满意度从高到低分为三个等级:
从乙地这20天PM2.5日平均浓度不超过40的天数中随机抽取两天,求这两天中至少有一天居民对空气质量满意度为“非常满意”的概率.

乙地20天PM2.5日平均浓度频数分布表
| PM2.5日平均浓度(微克/立方米) | [0,20] | (20,40] | (40,60] | (60,80] | (80,100] |
| 频数(天) | 2 | 3 | 4 | 6 | 5 |
(2)通过调查,该市市民对空气质量的满意度从高到低分为三个等级:
| 满意度等级 | 非常满意 | 满意 | 不满意 |
| PM2.5日平均浓度(微克/立方米) | 不超过20 | 大于20不超过60 | 超过60 |
15.若复数z=2-i+i2,则z2=( )
| A. | 2 | B. | 2i | C. | -2i | D. | $\sqrt{2}$ |
2.某转播商转播一场排球比赛,比赛采取五局三胜制,即一方先获得三局胜利比赛就结束,已知比赛双方实力相当,且每局比赛胜负都是相互独立的,若每局比赛转播商可以获得20万元的收益,则转播商获利不低于80万元的概率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{9}{16}$ |
19.把1,3,6,10,15,…这些数叫作“三角形数”,这是因为这些数目的点可以排成一个正三角形,则第15个三角形数是( )


| A. | 120 | B. | 105 | C. | 153 | D. | 91 |
 如图,在直三棱柱ABC-A1B1C1中,AB=AC=AA1=4,D为BB1上一点,E为AC上一点,且B1D=CE=1,BE=$\sqrt{7}$.
如图,在直三棱柱ABC-A1B1C1中,AB=AC=AA1=4,D为BB1上一点,E为AC上一点,且B1D=CE=1,BE=$\sqrt{7}$.