题目内容
2.某转播商转播一场排球比赛,比赛采取五局三胜制,即一方先获得三局胜利比赛就结束,已知比赛双方实力相当,且每局比赛胜负都是相互独立的,若每局比赛转播商可以获得20万元的收益,则转播商获利不低于80万元的概率是( )| A. | $\frac{3}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{9}{16}$ |
分析 由题意知转播商获利不低于80万元是指比赛打满4局或比赛打满5局,由此能求出转播商获利不低于80万元的概率.
解答 解:由题意知转播商获利不低于80万元是指比赛打满4局或比赛打满5局,
∴转播商获利不低于80万元的概率:
P=${C}_{3}^{2}(\frac{1}{2})^{2}(\frac{1}{2})$($\frac{1}{2}$)+${C}_{3}^{2}(\frac{1}{2})^{2}(\frac{1}{2})$(1-$\frac{1}{2}$)+${C}_{4}^{2}(\frac{1}{2})^{2}(\frac{1}{2})^{2}$×$\frac{1}{2}$+${C}_{4}^{2}(\frac{1}{2})^{2}(\frac{1}{2})^{2}$×(1-$\frac{1}{2}$)=$\frac{3}{4}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意n次独立重复试验中事件A恰好发生k次的概率计算公式的合理运用.

练习册系列答案
相关题目
12.已知$\overrightarrow a,\overrightarrow b$均为单位向量,它们的夹角为60°,那么|$\overrightarrow{a}$-2$\overrightarrow{b}$|等于( )
| A. | 2 | B. | $4-\sqrt{3}$ | C. | $\sqrt{13}$ | D. | $\sqrt{3}$ |
13.“x>-2”是“x2<4”( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.小品类是春节文艺晚会的重要节目,一调查机构为研究“喜欢收看春节文艺晚会小品类节目与地域文化是否有关”,在南北方不同地域随机抽取了100名市民进行调查,发现被调查对象的北方人有40名喜欢收看,有15名不喜欢收看;调查对象的南方人有20名喜欢收看,有25名不喜欢收看
(1)在被调查对象中,喜欢收看春节文艺晚会小品类节目的人数占各自地域的比例分别是多少?并初步判断喜欢收看春节文艺晚会小品类节目与地域是否有关?
(2)试根据题设数据完成2X2列联表,并判断是否有99.5%的把握认为喜欢收看春节文艺晚会小品类节目与地域文化有关
参考数据公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)},n=a+b+c+d$
临界值:
(1)在被调查对象中,喜欢收看春节文艺晚会小品类节目的人数占各自地域的比例分别是多少?并初步判断喜欢收看春节文艺晚会小品类节目与地域是否有关?
(2)试根据题设数据完成2X2列联表,并判断是否有99.5%的把握认为喜欢收看春节文艺晚会小品类节目与地域文化有关
参考数据公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)},n=a+b+c+d$
临界值:
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
11.如图下面程序框图运行的结果s=1320,那么判断框中应填入( )


| A. | k<10? | B. | k>10? | C. | k<11? | D. | k>11? |
12.某条公共汽车线路收支差额y与乘客量x的函数关系如图所示(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变车票价格,减少支出费用;建议(Ⅱ)不改变支出费用,提高车票价格,下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
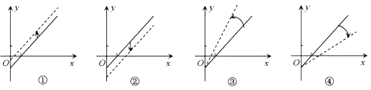

| A. | ①反映了建议(Ⅱ),③反映了建议(Ⅰ) | B. | ①反映了建议(Ⅰ),③反映了建议(Ⅱ) | ||
| C. | ②反映了建议(Ⅰ),④反映了建议(Ⅱ) | D. | ④反映了建议(Ⅰ),②反映了建议(Ⅱ) |
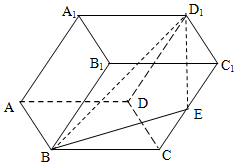 已知斜四棱柱平面ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,
已知斜四棱柱平面ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,