题目内容
20.一个均匀的正四面体的四个面分别写有1,2,3,4四个数字,现随机投掷两次,正四面体底面上的数字分别为x1,x2,记t=${({x_1}-3)^2}+{({x_2}-3)^2}$.(1)分别求出t取得最大值和最小值时的概率;
(2)求t≥4的概率.
分析 (1)当x1=x2=1时,t取得最大值;当x1=x2=3时,t取得最小值0.由此能求出结果.
(2)当t≥4时,t的取值为5,8.分别利用列举法求出当t=5时和当t=8时的概率,由此能求出t≥4的概率.
解答 解:(1)当x1=x2=1时,
t=(x1-3)2+(x2-3)2可取得最大值8,此时P=$\frac{1}{16}$;
当x1=x2=3时,t=${({x_1}-3)^2}+{({x_2}-3)^2}$可取得最小值0,此时P=$\frac{1}{16}$.
(2)当t≥4时,t的取值为5,8.
①当t=5时,(x1,x2)可能是:(2,1)、(1,4)、(1,2)、(4,1),
此时P=$\frac{1}{4}$;
②当t=8时,由(1)可知:P=$\frac{1}{16}$.
∴t≥4的概率为:$\frac{1}{4}+\frac{1}{16}$=$\frac{5}{16}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法和分类讨论思想的合理运用.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
10.设集合M={x|-3<x<2},N={x∈Z|-1≤x≤3},则M∩N等于( )
| A. | {0,1} | B. | {-1,0,1,2} | C. | {0,1,2} | D. | {-1,0,1} |
11.已知函数f(x)=2sin(2x-$\frac{π}{6}$)+a,a为常数
(1)求函数f(x)的最小正周期;
(2)若x∈[0,$\frac{π}{2}$]时,f(x)的最小值为-2,求a的值.
(1)求函数f(x)的最小正周期;
(2)若x∈[0,$\frac{π}{2}$]时,f(x)的最小值为-2,求a的值.
15.过正三棱柱底面一边所作的正三棱柱的截面是( )
| A. | 三角形 | B. | 三角形或梯形 | ||
| C. | 不是梯形的四边形 | D. | 梯形 |
12.已知$\overrightarrow a,\overrightarrow b$均为单位向量,它们的夹角为60°,那么|$\overrightarrow{a}$-2$\overrightarrow{b}$|等于( )
| A. | 2 | B. | $4-\sqrt{3}$ | C. | $\sqrt{13}$ | D. | $\sqrt{3}$ |
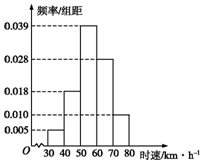 某时段内共有100辆汽车经过某一雷达地区,汽车时速的频率分布直方图如图所示,则时速不低于60km/h的汽车数量为( )
某时段内共有100辆汽车经过某一雷达地区,汽车时速的频率分布直方图如图所示,则时速不低于60km/h的汽车数量为( )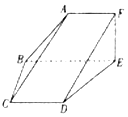 如图,平面ABEF⊥平面CBED,四边形ABEF为直角梯形,∠AFE=∠FEB=90°,四边形CBED为等腰梯形,CD∥BE,且BE=2AF=2CD=2BC=2EF=4.
如图,平面ABEF⊥平面CBED,四边形ABEF为直角梯形,∠AFE=∠FEB=90°,四边形CBED为等腰梯形,CD∥BE,且BE=2AF=2CD=2BC=2EF=4.