题目内容
7．下列函数中，既是偶函数又在区间（0，+∞）上单调递增的是（ ）| A． | $y=\frac{1}{x^2}$ | B． | y=${（\frac{1}{2}）}^{|x|}$ | C． | y=lg x | D． | y=|x|-1 |
分析 分别函数的奇偶性、单调性，即可得出结论．
解答 解：A中函数$y=\frac{1}{x^2}$是偶函数且在（0，+∞）上单调递减，故A错误；
B中函数是偶函数且在（0，+∞）上单调递减，故B错误；
C中函数不是偶函数，故C错误；
D中函数是偶函数且在（0，+∞）上单调递增，
故选D．
点评 本题考查函数的奇偶性、单调性，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
18．设正三棱锥A-BCD内接于球O，BC=1，E为AB的中点，AC⊥DE，则球的半径为（ ）
| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{6}}}{4}$ | D． | $\frac{{\sqrt{10}}}{4}$ |
2．已知F是抛物线C：y=2x2的焦点，点P（x，y）在抛物线C上，且x=1，则|PF|=（ ）
| A． | $\frac{9}{8}$ | B． | $\frac{3}{2}$ | C． | $\frac{17}{8}$ | D． | $\frac{5}{2}$ |
12．若实数x，y满足：$\left\{{\begin{array}{l}{y≥2x-2}\\{y≥-x+1}\\{y≤x+1}\end{array}}\right.$，则z=3x-y的最大值是（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
19．如表，将数字1，2，3，…，2n（n≥3）全部填入一个2行n列的表格中，每格填一个数字．第一行填入的数字依次为a1，a2，…，an，第二行填入的数字依次为b1，b2，…，bn．
记${S_n}=\sum_{i=1}^n{|{a_i}-{b_i}|}=\;|{a_1}-{b_1}|+|{a_2}-{b_2}|+…+|{a_n}-{b_n}|$．
（Ⅰ）当n=3时，若a1=1，a2=3，a3=5，写出S3的所有可能的取值；
（Ⅱ）给定正整数n．试给出a1，a2，…，an的一组取值，使得无论b1，b2，…，bn填写的顺序如何，Sn都只有一个取值，并求出此时Sn的值；
（Ⅲ）求证：对于给定的n以及满足条件的所有填法，Sn的所有取值的奇偶性相同．
记${S_n}=\sum_{i=1}^n{|{a_i}-{b_i}|}=\;|{a_1}-{b_1}|+|{a_2}-{b_2}|+…+|{a_n}-{b_n}|$．
| a1 | a2 | … | an |
| b1 | b2 | … | bn |
（Ⅱ）给定正整数n．试给出a1，a2，…，an的一组取值，使得无论b1，b2，…，bn填写的顺序如何，Sn都只有一个取值，并求出此时Sn的值；
（Ⅲ）求证：对于给定的n以及满足条件的所有填法，Sn的所有取值的奇偶性相同．
某商场为吸引顾客消费推出一项优惠活动．活动规则如下：消费额每满100元可转动如图所示的转盘一次，并获得相应金额的返券，假定指针等可能地停在任一位置．若指针停在A区域返券60元；停在B区域返券30元；停在C区域不返券．例如：消费218元，可转动转盘2次，所获得的返券金额是两次金额之和．
11．
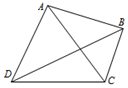蓝军和红军进行军事演练，蓝军在距离$\sqrt{3}$的军事基地C和D，测得红军的两支精锐部队分别在A处和B处，且∠ADB=30°，∠BDC=30°，∠DCA=60°，∠ACB=45°，如图所示，则红军这两支精锐部队间的距离是（ ）
蓝军和红军进行军事演练，蓝军在距离$\sqrt{3}$的军事基地C和D，测得红军的两支精锐部队分别在A处和B处，且∠ADB=30°，∠BDC=30°，∠DCA=60°，∠ACB=45°，如图所示，则红军这两支精锐部队间的距离是（ ）| A． | $\frac{{\sqrt{6}}}{2}$ | B． | $\sqrt{6}$ | C． | $\frac{3}{4}$ | D． | $\sqrt{3}$ |