题目内容
18.设正三棱锥A-BCD内接于球O,BC=1,E为AB的中点,AC⊥DE,则球的半径为( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{6}}}{4}$ | D. | $\frac{{\sqrt{10}}}{4}$ |
分析 证明AB,AC,AD两两垂直,将三棱锥扩充为正方体,正方体的对角线为球的直径,即可得出结论.
解答 解:由题意,AC⊥BD,
∵AC⊥DE,BD∩DE=D,
∴AC⊥平面ABD,
∴AB,AC,AD两两垂直,
将三棱锥扩充为正方体,正方体的对角线为球的直径,2R=$\sqrt{3}•\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}}{2}$,
∴球的半径为$\frac{\sqrt{6}}{4}$.
故选C.
点评 本题考查三棱锥外接球半径的求法,考查学生的计算能力,将三棱锥扩充为正方体,正方体的对角线为球的直径是关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
8.函数 f ( x)=$\frac{x}{lnx}$( x>1)单调递减区间是( )
| A. | (1,+∞) | B. | (1,e2) | C. | (e,+∞) | D. | (1,e) |
9.两个变量y与x的回归模型中,分别选择了4个不同模型,它们对应的回归系数r如下,其中变量之间线性相关程度最高的模型是( )
| A. | 模型1对应的r为-0.98 | B. | 模型2对应的r为0.80 | ||
| C. | 模型3对应的r为0.50 | D. | 模型4对应的r为-0.25 |
3.若集合$A=\left\{{y\left|{y={x^{\frac{1}{3}}}}\right.}\right\},B=\left\{{x\left|{y=ln({x-1})}\right.}\right\}$,则A∩B=( )
| A. | [1,+∞) | B. | (0,1) | C. | (1,+∞) | D. | (-∞,1) |
10.若一个几何体的三视图都是如图所示的边长为2的正方形,则该几何体的外接球的表面积是( )

| A. | π | B. | 2π | C. | 4π | D. | 8π |
7.下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是( )
| A. | $y=\frac{1}{x^2}$ | B. | y=${(\frac{1}{2})}^{|x|}$ | C. | y=lg x | D. | y=|x|-1 |
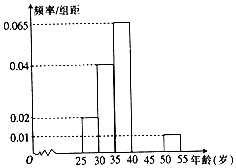 某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为[25,30),[30,35),[35,40),[40,45),[45,50),[50,55],如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组[40,45)的人数为4人.
某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为[25,30),[30,35),[35,40),[40,45),[45,50),[50,55],如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组[40,45)的人数为4人.