题目内容
12.若实数x,y满足:$\left\{{\begin{array}{l}{y≥2x-2}\\{y≥-x+1}\\{y≤x+1}\end{array}}\right.$,则z=3x-y的最大值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 根据题意先画出满足约束条件的平面区域,然后分析平面区域里各个角点,令z=3x-y,进一步求出目标函数z=3x-y的最大值.
解答  解:满足约束条件:$\left\{{\begin{array}{l}{y≥2x-2}\\{y≥-x+1}\\{y≤x+1}\end{array}}\right.$的平面区域如图所示:
解:满足约束条件:$\left\{{\begin{array}{l}{y≥2x-2}\\{y≥-x+1}\\{y≤x+1}\end{array}}\right.$的平面区域如图所示:
由$\left\{\begin{array}{l}{y=2x-2}\\{y=x+1}\end{array}\right.$得A(3,4)平移目标函数,当目标函数经过A时,z取得最大值.
代入得z=3×3-4=5,
当x=3,y=4时,3x-y有最大值5.
故选:C.
点评 在解决线性规划的小题时,利用目标函数的几何意义求解,也常用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证,求出最优解.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
3.若集合$A=\left\{{y\left|{y={x^{\frac{1}{3}}}}\right.}\right\},B=\left\{{x\left|{y=ln({x-1})}\right.}\right\}$,则A∩B=( )
| A. | [1,+∞) | B. | (0,1) | C. | (1,+∞) | D. | (-∞,1) |
7.下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是( )
| A. | $y=\frac{1}{x^2}$ | B. | y=${(\frac{1}{2})}^{|x|}$ | C. | y=lg x | D. | y=|x|-1 |
15.已知等差数列{an}的公差d≠0,且a1,a3,a13成等比数列,若a1=1,Sn为数列{an}的前n项和,则$\frac{2{S}_{n}+16}{{a}_{n}+3}$的最小值为( )
| A. | 4 | B. | 3 | C. | 2$\sqrt{3}$-2 | D. | 2 |
16.若a,b∈R,则复数(a2-6a+10)+(-b2+4b-5)i对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
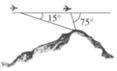 如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔15000 m,速度为1000 km/h,飞行员先看到山顶的俯角为15°,经过108s后又看到山顶的俯角为75°,则山顶的海拔高度为15-10$\sqrt{3}$km.
如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔15000 m,速度为1000 km/h,飞行员先看到山顶的俯角为15°,经过108s后又看到山顶的俯角为75°,则山顶的海拔高度为15-10$\sqrt{3}$km.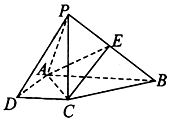 如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,AB=2AD=2CD=4,PC=2a,E是PB的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,AB=2AD=2CD=4,PC=2a,E是PB的中点.