��Ŀ����
10�� ij�̳�Ϊ�����˿������Ƴ�һ���Żݻ����������£����Ѷ�ÿ��100Ԫ��ת����ͼ��ʾ��ת��һ�Σ��������Ӧ���ķ�ȯ���ٶ�ָ��ȿ��ܵ�ͣ����һλ�ã���ָ��ͣ��A����ȯ60Ԫ��ͣ��B����ȯ30Ԫ��ͣ��C����ȯ�����磺����218Ԫ����ת��ת��2�Σ�����õķ�ȯ��������ν��֮�ͣ�
ij�̳�Ϊ�����˿������Ƴ�һ���Żݻ����������£����Ѷ�ÿ��100Ԫ��ת����ͼ��ʾ��ת��һ�Σ��������Ӧ���ķ�ȯ���ٶ�ָ��ȿ��ܵ�ͣ����һλ�ã���ָ��ͣ��A����ȯ60Ԫ��ͣ��B����ȯ30Ԫ��ͣ��C����ȯ�����磺����218Ԫ����ת��ת��2�Σ�����õķ�ȯ��������ν��֮�ͣ�������ijλ�˿�����128Ԫ����ȯ������30Ԫ�ĸ��ʣ�
������ijλ�˿�ǡ������280Ԫ��������������˻������÷�ȯ�Ľ���ΪX��Ԫ������X=60ʱ�ĸ��ʣ�
���� ����ȯ������30Ԫ����ָ��ͣ��A�����ͣ��B����ָ��ͣ���ĸ�������¼��ǻ���ģ��ȸ��ݼ��θ�������ͣ�ڸ�������ĸ��ʣ����û����¼��ĸ��ʹ�ʽ�õ������
������ijλ�˿�ǡ������280Ԫ���ù˿Ϳ�ת��ת��2�Σ��������X=60ʱ�ĸ��ʣ�
��� �⣺��ָ������A��B��C����ֱ��Ϊ�¼�A��B��C��
��P��A��=$\frac{1}{6}$��P��B��=$\frac{1}{3}$��P��C��=$\frac{1}{2}$��
��������ȯ������30Ԫ����ָ������A��B����P=P��A��+P��B��=$\frac{1}{2}$��
������128Ԫ�Ĺ˿ͣ���ȯ������30Ԫ�ĸ���$\frac{1}{2}$��
����������ã��ù˿Ϳ�ת��ת��2�Σ�P��X=60��=$\frac{1}{2}��\frac{1}{6}��2+\frac{1}{3}��\frac{1}{3}$=$\frac{5}{18}$
���� ���⿼����ʵļ��㣬����������ѧ֪ʶ���ʵ�����⣬����ѧ�������������������������е��⣮

��ϰ��ϵ�д�
�����Ŀ
7�����к����У�����ż�����������䣨0��+�ޣ��ϵ����������ǣ�������
| A�� | $y=\frac{1}{x^2}$ | B�� | y=${��\frac{1}{2}��}^{|x|}$ | C�� | y=lg x | D�� | y=|x|-1 |
15����֪�Ȳ�����{an}�Ĺ���d��0����a1��a3��a13�ɵȱ����У���a1=1��SnΪ����{an}��ǰn��ͣ���$\frac{2{S}_{n}+16}{{a}_{n}+3}$����СֵΪ��������
| A�� | 4 | B�� | 3 | C�� | 2$\sqrt{3}$-2 | D�� | 2 |
19����֪����������ص���������x��y֮���һ�����������
�һع鷽����y=0.65x+2.7����m=��������
| x | 0 | 1 | 2 | 3 | 4 |
| y | 2 | 4.2 | 4.5 | 4.6 | m |
| A�� | 5.6 | B�� | 5.3 | C�� | 5.0 | D�� | 4.7 |
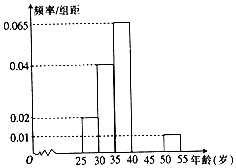 ij��Ϊ��ѡ��ȫ���������С�����200��־Ը���������ȡ40��־Ը�߲μӽֵ������ල�������ͳ����Щ־Ը�ߵ��������25���55��֮�䣬Ϊ���㰲����������־Ը�߰������С����ֳ����飬����Ϊ[25��30����[30��35����[35��40����[40��45����[45��50����[50��55]����ͼ�ǰ����������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣���֪������[40��45��������Ϊ4�ˣ�
ij��Ϊ��ѡ��ȫ���������С�����200��־Ը���������ȡ40��־Ը�߲μӽֵ������ල�������ͳ����Щ־Ը�ߵ��������25���55��֮�䣬Ϊ���㰲����������־Ը�߰������С����ֳ����飬����Ϊ[25��30����[30��35����[35��40����[40��45����[45��50����[50��55]����ͼ�ǰ����������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣���֪������[40��45��������Ϊ4�ˣ�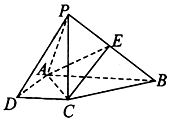 ��ͼ��������P-ABCD�У��ı���ABCD��ֱ�����Σ�AB��AD��AB��CD��PC�͵���ABCD��AB=2AD=2CD=4��PC=2a��E��PB���е㣮
��ͼ��������P-ABCD�У��ı���ABCD��ֱ�����Σ�AB��AD��AB��CD��PC�͵���ABCD��AB=2AD=2CD=4��PC=2a��E��PB���е㣮 ������PDC���ڵ�ƽ���볤����ABCD���ڵ�ƽ�洹ֱ��PD=PC=4��$AB=4\sqrt{2}$��BC=3����E��CD�ߵ��е㣬��F��G�ֱ����߶�AB��BC�ϣ���AF=2FB��CG=2GB��
������PDC���ڵ�ƽ���볤����ABCD���ڵ�ƽ�洹ֱ��PD=PC=4��$AB=4\sqrt{2}$��BC=3����E��CD�ߵ��е㣬��F��G�ֱ����߶�AB��BC�ϣ���AF=2FB��CG=2GB��