题目内容
11.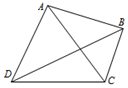 蓝军和红军进行军事演练,蓝军在距离$\sqrt{3}$的军事基地C和D,测得红军的两支精锐部队分别在A处和B处,且∠ADB=30°,∠BDC=30°,∠DCA=60°,∠ACB=45°,如图所示,则红军这两支精锐部队间的距离是( )
蓝军和红军进行军事演练,蓝军在距离$\sqrt{3}$的军事基地C和D,测得红军的两支精锐部队分别在A处和B处,且∠ADB=30°,∠BDC=30°,∠DCA=60°,∠ACB=45°,如图所示,则红军这两支精锐部队间的距离是( )| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $\sqrt{6}$ | C. | $\frac{3}{4}$ | D. | $\sqrt{3}$ |
分析 先在△BCD中,求得BC的长,再求得AC的长,最后在△ABC中利用余弦定理,即可求得AB的长,即伊军这两支精锐部队的距离.
解答 解:在△BCD中,DC=$\sqrt{3}$,∠DBC=180°-30°-60°-45°=45°,∠BDC=30°,
∴$\frac{\sqrt{3}}{sin45°}=\frac{BC}{sin30°}$,∴BC=$\frac{\sqrt{6}}{2}$.
在等边三角形ACD中,AC=AD=CD=$\sqrt{3}$,
在△ABC中,AC=$\sqrt{3}$,BC=$\frac{\sqrt{6}}{2}$,∠ACB=45°
∴AB=$\sqrt{3+\frac{3}{2}-2×\sqrt{3}×\frac{\sqrt{6}}{2}×\frac{\sqrt{2}}{2}}$=$\frac{\sqrt{6}}{2}$.
故选A.
点评 本题重点考查正弦定理与余弦定理的运用,选择三角形,合理运用定理是解题的关键.

练习册系列答案
相关题目
7.下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是( )
| A. | $y=\frac{1}{x^2}$ | B. | y=${(\frac{1}{2})}^{|x|}$ | C. | y=lg x | D. | y=|x|-1 |
6.某地震观测站对地下水位的变化和发生地震的情况共进行了n=1 700次观测,列联表如下:
问观测结果是否说明地下水位的变化与地震的发生相关?
| Y X | 有震 | 无震 | 合计 |
| 水位有变化 | 100 | 900 | 1 000 |
| 水位无变化 | 80 | 620 | 7 00 |
| 合计 | 180 | 1520 | 1700 |
| P(X2≥x0) | 0.15 | 0.1 | 0.05 |
| x0 | 2.072 | 2.706 | 3.841 |
16.若a,b∈R,则复数(a2-6a+10)+(-b2+4b-5)i对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,$AB=4\sqrt{2}$,BC=3.点E是CD边的中点,点F、G分别在线段AB、BC上,且AF=2FB,CG=2GB.
三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,$AB=4\sqrt{2}$,BC=3.点E是CD边的中点,点F、G分别在线段AB、BC上,且AF=2FB,CG=2GB. 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈(0,1),给出以下命题:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈(0,1),给出以下命题: