题目内容
17.已知圆x2+y2=1和圆外一点P(1,2),过点P作圆的切线,则切线方程为x=1或3x-4y+5=0.分析 根据直线和圆相切的等价条件转化为圆心到直线的距离等于半径即可得到结论.
解答 解:圆心坐标为(0,0),半径为1,
∵点P(1,2)在圆外,
∴若直线斜率k不存在,
则直线方程为x=1,圆心到直线的距离为1,满足相切.
若直线斜率存在设为k,
则直线方程为y-2=k(x-1),即kx-y+2-k=0,
则圆心到直线kx-y+2-k=0的距离等于半径1,
即d=$\frac{|2-k|}{\sqrt{1+{k}^{2}}}$=1,
解得k=$\frac{3}{4}$,此时直线方程为3x-4y+5=0,
综上切线方程为x=1或3x-4y+5=0,
故答案为:x=1或3x-4y+5=0.
点评 本题主要考查直线和圆的位置关系的应用,根据相切的等价条件是解决本题的关键.注意讨论直线的斜率是否存在.

练习册系列答案
相关题目
7.椭圆my2+x2=1的一个顶点在抛物线$y=\frac{1}{2}{x^2}$的准线上,则椭圆的离心率( )
| A. | $\frac{{\sqrt{63}}}{8}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 4 | D. | $\frac{{\sqrt{5}}}{2}$ |
8.函数 f ( x)=$\frac{x}{lnx}$( x>1)单调递减区间是( )
| A. | (1,+∞) | B. | (1,e2) | C. | (e,+∞) | D. | (1,e) |
5.已知函数f ( x)=ax3+bx2+cx+d 的图象如图所示,则$\frac{b+1}{a+1}$的取值范围是( )
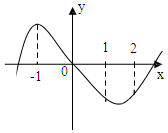

| A. | (-$\frac{3}{2}$,$\frac{1}{2}$ ) | B. | (-$\frac{2}{5}$,1) | C. | (-$\frac{1}{2}$,$\frac{3}{2}$) | D. | (-$\frac{3}{2}$,1) |
12.已知数列{an}是等差数列,a1=cot585°,a6=11a1,设Sn为数列{(-1)nan}的前n项和,则S2017=( )
| A. | 3022 | B. | -3022 | C. | 2017 | D. | -2017 |
9.两个变量y与x的回归模型中,分别选择了4个不同模型,它们对应的回归系数r如下,其中变量之间线性相关程度最高的模型是( )
| A. | 模型1对应的r为-0.98 | B. | 模型2对应的r为0.80 | ||
| C. | 模型3对应的r为0.50 | D. | 模型4对应的r为-0.25 |
7.下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是( )
| A. | $y=\frac{1}{x^2}$ | B. | y=${(\frac{1}{2})}^{|x|}$ | C. | y=lg x | D. | y=|x|-1 |
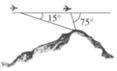 如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔15000 m,速度为1000 km/h,飞行员先看到山顶的俯角为15°,经过108s后又看到山顶的俯角为75°,则山顶的海拔高度为15-10$\sqrt{3}$km.
如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔15000 m,速度为1000 km/h,飞行员先看到山顶的俯角为15°,经过108s后又看到山顶的俯角为75°,则山顶的海拔高度为15-10$\sqrt{3}$km.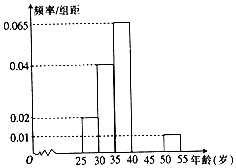 某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为[25,30),[30,35),[35,40),[40,45),[45,50),[50,55],如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组[40,45)的人数为4人.
某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为[25,30),[30,35),[35,40),[40,45),[45,50),[50,55],如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组[40,45)的人数为4人.