题目内容
15.已知函数$f(x)=\frac{1}{x+1}$,点O为坐标原点,点${A_n}({n,f(n)})({n∈{N^*}})$,向量$\vec i=({0,1})$,θn是向量$\overrightarrow{O{A}_{n}}$与$\vec i$的夹角,则$\frac{{cos{θ_1}}}{{sin{θ_1}}}+\frac{{cos{θ_2}}}{{sin{θ_2}}}+…+\frac{{cos{θ_{2017}}}}{{sin{θ_{2017}}}}$的值为$\frac{2017}{2018}$.分析 求得$\overrightarrow{O{A}_{n}}$=(n,$\frac{1}{n+1}$),运用向量的夹角公式可得cosθn,再求sinθn,可得$\frac{cos{θ}_{n}}{sin{θ}_{n}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,运用裂项相消求和,即可得到所求和.
解答 解:函数$f(x)=\frac{1}{x+1}$,
可得An(n,$\frac{1}{n+1}$),$\overrightarrow{O{A}_{n}}$=(n,$\frac{1}{n+1}$),
cosθn=$\frac{\overrightarrow{O{A}_{n}}•\overrightarrow{i}}{|\overrightarrow{O{A}_{n}}|•|\overrightarrow{i}|}$=$\frac{\frac{1}{n+1}}{\sqrt{{n}^{2}+\frac{1}{(n+1)^{2}}}}$=$\frac{1}{\sqrt{{n}^{2}(n+1)^{2}+1}}$,
sinθn=$\sqrt{1-co{s}^{2}{θ}_{n}}$=$\frac{n(n+1)}{\sqrt{{n}^{2}(n+1)^{2}+1}}$,
可得$\frac{cos{θ}_{n}}{sin{θ}_{n}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
则$\frac{{cos{θ_1}}}{{sin{θ_1}}}+\frac{{cos{θ_2}}}{{sin{θ_2}}}+…+\frac{{cos{θ_{2017}}}}{{sin{θ_{2017}}}}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2017}$-$\frac{1}{2018}$
=1-$\frac{1}{2018}$=$\frac{2017}{2018}$.
故答案为:$\frac{2017}{2018}$.
点评 本题考查向量的夹角公式,同角的平方关系,以及数列的求和方法:裂项相消求和,考查化简整理的运算能力,属于中档题.

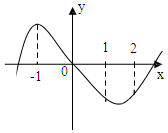
| A. | (-$\frac{3}{2}$,$\frac{1}{2}$ ) | B. | (-$\frac{2}{5}$,1) | C. | (-$\frac{1}{2}$,$\frac{3}{2}$) | D. | (-$\frac{3}{2}$,1) |
| A. | [1,+∞) | B. | (0,1) | C. | (1,+∞) | D. | (-∞,1) |
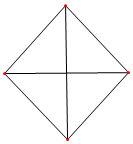
| A. | π | B. | 2π | C. | 4π | D. | 8π |
| A. | $y=\frac{1}{x^2}$ | B. | y=${(\frac{1}{2})}^{|x|}$ | C. | y=lg x | D. | y=|x|-1 |
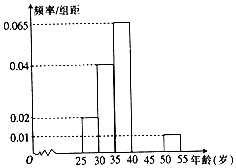 某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为[25,30),[30,35),[35,40),[40,45),[45,50),[50,55],如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组[40,45)的人数为4人.
某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为[25,30),[30,35),[35,40),[40,45),[45,50),[50,55],如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组[40,45)的人数为4人.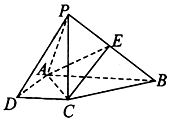 如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,AB=2AD=2CD=4,PC=2a,E是PB的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,AB=2AD=2CD=4,PC=2a,E是PB的中点.