题目内容
已知:A={(x,y)|x+y=0},B={(x,y)|x-y=2},则A∩B= .
考点:交集及其运算
专题:集合
分析:直接联立方程组求解两直线的交点得答案.
解答:
解:∵A={(x,y)|x+y=0},B={(x,y)|x-y=2},
则A∩B={(x,y)|
}={(1,-1)}.
故答案为:{(1,-1)}.
则A∩B={(x,y)|
|
故答案为:{(1,-1)}.
点评:本题考查了交集及其运算,考查了方程组的解法,是基础题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
已知集合M={x|-1≤x<2},N={x|-1<x-a≤0},若M∩N≠∅,则a的取值范围是( )
| A、a<-1,或a≥3 |
| B、-3<a≤1 |
| C、-3≤a≤3 |
| D、-1≤a<3 |
数列1,x,x2,…xn-1前n项的和Sn=( )
A、
| ||
B、
| ||
C、
| ||
| D、以上均不对 |
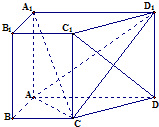 如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD是直角梯形,其中AB⊥AD,AB=BC=1且AD=
如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD是直角梯形,其中AB⊥AD,AB=BC=1且AD=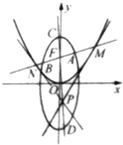 已知椭圆
已知椭圆