题目内容
计算：2lg（
+
）
3+
|
3-
|
考点：对数的运算性质,根式与分数指数幂的互化及其化简运算
专题：计算题,函数的性质及应用
分析：运用对数的运算法则logamn=nlogam，以及根式的性质，即可求得．
解答：
解：2lg（
+
）=lg（
+
）2
=lg（3+
+3-
+2
）
=lg（6+4）
=lg10=1．
3+
|
3-
|
3+
|
3-
|
=lg（3+
| 5 |
| 5 |
| 9-5 |
=lg（6+4）
=lg10=1．
点评：本题考查了根式的运算法则、对数的运算法则，属于基础题．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
相关题目
设Sn是等差数列{an}的前n项和，若
=
，则
=（ ）
| a4 |
| a2 |
| 5 |
| 9 |
| S7 |
| S3 |
| A、1 | ||
| B、-1 | ||
| C、2 | ||
D、
|
阅读所示的流程图，若输入的a，b，c分别是35，52，63，则输出的a，b，c分别是（ ）
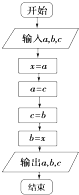
| A、63，35，52 |
| B、35，52，63 |
| C、63，52，35 |
| D、35，63，52 |
如图所示的是一个算法的程序框图，已知a1=3，输出的b=7，则a2等于（ ）
| A、9 | B、10 | C、11 | D、12 |