题目内容
判断函数f（x）=
的奇偶性．
| x(3x-1) |
| 3x+1 |
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：根据函数的奇偶性的定义，即可得到结论．
解答：
解：函数的定义域为R，
则f（-x）=
=
=
=f（x），
则函数f（x）是偶函数．
则f（-x）=
| -x(3-x-1) |
| 3-x+1 |
| -x(1-3x) |
| 1+3x |
| x(3x-1) |
| 3x+1 |
则函数f（x）是偶函数．
点评：本题主要考查函数奇偶性的判断，根据奇偶性的定义是解决本题的关键．
练习册系列答案
相关题目
设α，β是锐角，且cosα=
，sin（α+β）=
，则β=（ ）
| 1 |
| 7 |
5
| ||
| 14 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设Sn是等差数列{an}的前n项和，若
=
，则
=（ ）
| a4 |
| a2 |
| 5 |
| 9 |
| S7 |
| S3 |
| A、1 | ||
| B、-1 | ||
| C、2 | ||
D、
|
阅读所示的流程图，若输入的a，b，c分别是35，52，63，则输出的a，b，c分别是（ ）
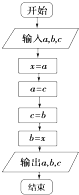
| A、63，35，52 |
| B、35，52，63 |
| C、63，52，35 |
| D、35，63，52 |