题目内容
 已知椭圆
已知椭圆| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
(1)求椭圆的方程.
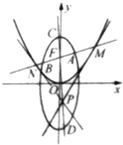
(2)过点P(t,-1)作抛物线的两条切线,切点分别为M,N,直线MN与椭圆交于A,B两点,直线PF与椭圆交于C,D两点,如图所示.
①求直线MN的方程.
②求四边形ABCD的面积的最大值和最小值.
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)求出抛物线x2=4y的焦点F(0,1),则c=1,再由椭圆的离心率公式,即可得到a,再由a,b,c的关系,求出b,即可得到椭圆方程;
(2))①设出切点,求出函数y=
x2的导数,求得切线的斜率,求出切线方程,得到交点P,即可得到MN的方程;
②求出直线PF的方程,得到MN⊥PF,联立直线方程和椭圆方程,消去y,运用韦达定理和弦长公式,得到AB,CD的长,再由面积公式S=
|AB|•|CD|,化简整理,讨论t=0,t≠0,分别求出最值即可,注意运用基本不等式.
(2))①设出切点,求出函数y=
| 1 |
| 4 |
②求出直线PF的方程,得到MN⊥PF,联立直线方程和椭圆方程,消去y,运用韦达定理和弦长公式,得到AB,CD的长,再由面积公式S=
| 1 |
| 2 |
解答:
解:(1)抛物线x2=4y的焦点F(0,1),则c=1,
∵椭圆的离心率为
,∴
=
,
∴a=
,∴b=1,
∴椭圆的方程为
+x2=1;
(2)①设M(x1,y1)、N(x2,y2),y=
x2的导数y′=
x,
y1=
x12,y2=
x22,
则切线PM:y-
=
x1(x-x1),即y=
x1x-
,
同理切线PN:y=
x2x-
,
联立求得P(
,
),则x1+x2=2t,x1x2=-4,
∴直线MN的方程为y=
x-
,即y=
tx+1,
②直线PF:y-1=-
(x-6),即y=-
x+1,
∵
t•(-
)=-1,∴MN⊥PF,
由
消去y,得,(8+t2)x2+4tx-4=0,显然△>0,
x1+x2=-
,x1x2=
,2
则弦长AB=
•
,
同理由
消去y,可得弦长CD=
•
,
则有四边形ABCD的面积S=
|AB|•|CD|=
=2•
=2•
,
故当t=0时,面积S有最大值2,
当t≠0时,S=2•
,当且仅当t2=
,即t=±2时,S最小,且为
.
∵椭圆的离心率为
| ||
| 2 |
| c |
| a |
| ||
| 2 |
∴a=
| 2 |
∴椭圆的方程为
| y2 |
| 2 |
(2)①设M(x1,y1)、N(x2,y2),y=
| 1 |
| 4 |
| 1 |
| 2 |
y1=
| 1 |
| 4 |
| 1 |
| 4 |
则切线PM:y-
| x12 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| x12 |
| 4 |
同理切线PN:y=
| 1 |
| 2 |
| x22 |
| 4 |
联立求得P(
| x1+x2 |
| 2 |
| x1x2 |
| 4 |
∴直线MN的方程为y=
| x1+x2 |
| 4 |
| x1x2 |
| 4 |
| 1 |
| 2 |
②直线PF:y-1=-
| 2 |
| t |
| 2 |
| t |
∵
| 1 |
| 2 |
| 2 |
| t |
由
|
x1+x2=-
| 4t |
| 8+t2 |
| -4 |
| 8+t2 |
则弦长AB=
1+
|
|
同理由
|
1+
|
|
则有四边形ABCD的面积S=
| 1 |
| 2 |
| 2(4+t2)2 |
| (2+t2)(8+t2) |
=2•
| t4+8t2+16 |
| t4+10t2+16 |
| 1 | ||
1+
|
故当t=0时,面积S有最大值2,
当t≠0时,S=2•
| 1 | ||||
1+
|
| 16 |
| t2 |
| 16 |
| 9 |
点评:本题考查椭圆的方程和性质,考查联立直线方程和椭圆方程,运用韦达定理,以及弦长公式的运用,同时考查运用导数求切线的方程,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
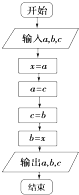
阅读所示的流程图,若输入的a,b,c分别是35,52,63,则输出的a,b,c分别是( )

| A、63,35,52 |
| B、35,52,63 |
| C、63,52,35 |
| D、35,63,52 |
若函数f(x)的图象上存在不同两点A,B,设线段AB的中点为M(x0,y0),使得f(x)在点(x0,f(x0))处的切线l与直线AB平行或重合,则称切线l为函数f(x)的“平衡切线”.则函数f(x)=2aln(x+1)+x2-2x的“平衡切线”的条数为( )
| A、2条或无数条 |
| B、1条或无数条 |
| C、0条或无数条 |
| D、2条或0条 |
在空间四边形ABCD中,AB、BC、CD、DA上分别取E、F、G、H四点,如果EH、FG交于一点P,则( )
| A、P一定在直线BD上 |
| B、P一定在直线AC上 |
| C、P在直线AC或BD上 |
| D、P既不在直线BD上,也不在AC上 |
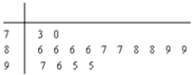 某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数,现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):
某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数,现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):