题目内容
5.已知函数f(x)=$\frac{x}{1+|x|}$(x∈R)时,则下列所有正确命题的序号是①②③.①若任意x∈R,则等式f(-x)+f(x)=0恒成立;
②存在m∈(0,1),使得方程|f(x)|=m有两个不等实数根;
③任意x1,x2∈R,若x1≠x2,则一定有f(x1)≠f(x2)
④存在k∈(1,+∞),使得函数g(x)=f(x)-kx在R上有三个零点.
分析 根据奇函数的定义判断①,根据函数的图象判断②③④
解答 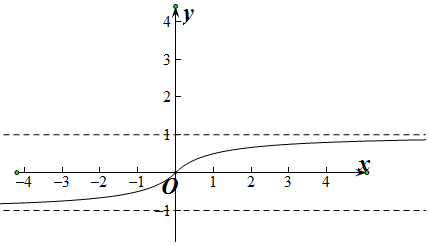 解:f(x)=$\frac{x}{1+|x|}$(x∈R)的图象为
解:f(x)=$\frac{x}{1+|x|}$(x∈R)的图象为
对于①,函数的定义域为R,f(-x)=$\frac{-x}{1+|-x|}$=-$\frac{x}{1+|x|}$=-f(x),
f(x)+f(-x)=0恒成立,故①正确,
对于②,由图象可知,函数的值域为(-1,1),
故存在m∈(0,1),使得方程|f(x)|=m有两个不等实数根,故②正确,
对于③由图象可知,函数在R上单调递增,故任意x1,x2∈R,若x1≠x2,则一定有f(x1)≠f(x2),故③正确,
对于④,分别画出y=f(x)与y=kx的图象,由图象可知,使得函数g(x)=f(x)-kx在R上有一个零点,故④错误,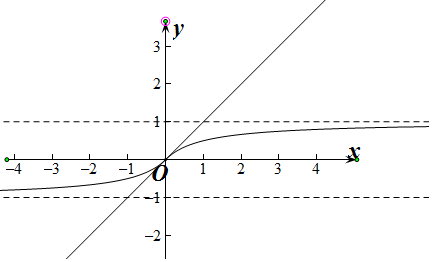
故答案为:①②③
点评 本题考查了函数图象及其性质,关键是绘制函数图象,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
16.双曲线$\frac{{x}^{2}}{5}-\frac{{y}^{2}}{2}$=1与椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{9}$=1(a>0)有相同的焦点,则a的值为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{10}$ | C. | 4 | D. | $\sqrt{34}$ |
13.下列命题中假命题是( )
| A. | ?x∈R,lgx=0 | B. | ?x∈R,sinx+cosx=$\sqrt{3}$ | ||
| C. | ?x∈R,x2+1≥2x | D. | ?x∈R,2x>0 |
20.若a>b>1,0<c<1,则( )
| A. | ac<bc | B. | abc<bac | C. | ca<cb | D. | logac<logbc |
4.若$\overline z$=$\frac{i}{1+i}$,则z•$\overline z$=( )
| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{1}{2}$ |
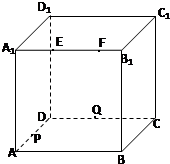 如图,正方体ABCD一A1B1C1D1的棱长为2,动点E,F在棱A1B1上,且EF=1,动点Q在棱CD上,P是棱AD中点,R是棱DDl的中点,则以下结论:
如图,正方体ABCD一A1B1C1D1的棱长为2,动点E,F在棱A1B1上,且EF=1,动点Q在棱CD上,P是棱AD中点,R是棱DDl的中点,则以下结论: