题目内容
3.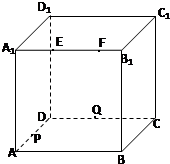 如图,正方体ABCD一A1B1C1D1的棱长为2,动点E,F在棱A1B1上,且EF=1,动点Q在棱CD上,P是棱AD中点,R是棱DDl的中点,则以下结论:
如图,正方体ABCD一A1B1C1D1的棱长为2,动点E,F在棱A1B1上,且EF=1,动点Q在棱CD上,P是棱AD中点,R是棱DDl的中点,则以下结论:①四面体PEFQ的体积为定值;
②异面直线PE与QF的所成角的大小为定值;
③过P点有且只有一条直线与直线BB1和C1D1都平行;
④过P点有且只有一个平面与直线BB1和C1D1都平行;
⑤过点B,P,R的平面截该正方体所得的截面是五边形.
其中正确结论的序号是①④.
分析 根据正方体的几何特征,逐一分析五个命题的真假,可得答案.
解答 解:∵CD∥平面EFP,
∴Q到平面EFP的距离等于D到平面EFP的距离$\frac{2\sqrt{5}}{5}$.
而S△EFP=$\frac{1}{2}$×1×$\sqrt{5}$=$\frac{\sqrt{5}}{2}$.
∴VQ-EFP=$\frac{1}{3}$
故①正确,
建立如图所示的坐标系,
设E点坐标为(2,m,2),F点坐标为(2,m+1,2),
则$\overrightarrow{PE}$=(1,m,2),$\overrightarrow{QF}$=(2,m,2),
故异面直线PE与QF的所成角的余弦值为:$\frac{{m}^{2}+6}{\sqrt{5+{m}^{2}}\sqrt{8+{m}^{2}}}$不是常量,
故②异面直线PE与QF的所成角的大小为定值,错误;
直线BB1和C1D1不平行;
故③过P点有且只有一条直线与直线BB1和C1D1都平行,错误;
过P点有且只有一个平面与前后表面都平行的平面直线BB1和C1D1都平行;
故④正确;
过点B,P,R的平面与前表面和上表面不相交,
故该平面截该正方体所得的截面是四边形,
故⑤错误.
故答案为:①④
点评 本题以命题的真假与应用为载体,考查了正方体的几何特征,棱锥的体积,异面直线夹角,空间直线与平面关系,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知直线:bx+ay=0与直线:x-2y+2=0垂直,则二次函数f(x)=ax2-bx+a的说法正确的是( )
| A. | f(x)开口方向朝上 | B. | f(x)的对称轴为x=1 | C. | f(x)在(-∞,-1)上递增 | D. | f(x)在(-∞,-1)上递减 |
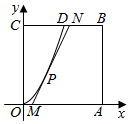 某地要建造一个边长为2(单位:km)的正方形市民休闲公园OABC,将其中的区域ODC开挖成一个池塘,如图建立平面直角坐标系后,点D的坐标为(1,2),曲线OD是函数y=ax2图象的一部分,对边OA上一点M在区域OABD内作一次函数y=kx+b(k>0)的图象,与线段DB交于点N(点N不与点D重合),且线段MN与曲线OD有且只有一个公共点P,四边形MABN为绿化风景区:
某地要建造一个边长为2(单位:km)的正方形市民休闲公园OABC,将其中的区域ODC开挖成一个池塘,如图建立平面直角坐标系后,点D的坐标为(1,2),曲线OD是函数y=ax2图象的一部分,对边OA上一点M在区域OABD内作一次函数y=kx+b(k>0)的图象,与线段DB交于点N(点N不与点D重合),且线段MN与曲线OD有且只有一个公共点P,四边形MABN为绿化风景区: